题目内容
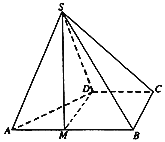
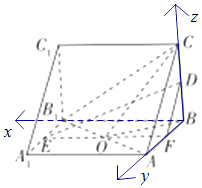
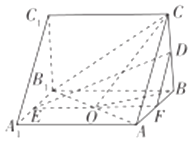
【题目】在如图所示的三棱锥ABC﹣A1B1C1中,AA1⊥底面ABC,D,E分别是BC,A1B1的中点. 
(1)求证:DE∥平面ACC1A1;
(2)若AB⊥BC,AB=BC,∠ACB1=60°,求直线BC与平面AB1C所成角的正切值.
【答案】
(1)解:取AB的中点F,连接DF,EF
在△ABC中,因为D,F分别为BC,AB的中点,
所以DF∥AC(中位线),
又∵DF平面ACC1A1,AC平面ACC1A1,
所以DF∥平面ACC1A1
在矩形ABB1A1中,因为E,F分别为A1B1,AB的中点,
∴EF∥AA1(中位线),
又∵EF平面 ACC1A1,AA1平面ACC1A1,
∴EF∥平面ACC1A1
∵DF∩EF=F,
∴平面DEF∥平面ACC1A1
∵DE平面DEF,
∴DE∥平面ACC1A1
(2)解:解法一:
∵三棱柱ABC﹣A1B1C1为直三棱柱,
∴BC⊥BB1,
又AB⊥BC,AB∩BB1=B,
∴BC⊥平面ABB1A1,
∵AB=BC,BB1=BB1,
∴△ABB1≌△CBB1
∴AB1=CB1,又 ![]() ,
,
∴△AB1C为正三角形,
∴ ![]() ,∴BB1=AB
,∴BB1=AB
取AB1的中点O,连接BO,CO,
∴AB1⊥BO,AB1⊥CO,
∴AB1⊥平面BCO,
∴平面AB1C⊥平面BCO,点B在平面AB1C上的射影在CO上,
∴∠BCO即为直线BC与平面AB1C所成角
在Rt△BCO中, ![]() ,
,
∴ ![]()
解法二:由题知BB1,BA,BC两两互相垂直,故建立空间直角坐标线如图,
并设AB=2,BB1=t,
则A(0,2,0),C(0,0,2),B1(t,0,0)(t>0)
∴ ![]() ,
, ![]()
∵ ![]() ,∴
,∴ ![]() =60°
=60°
∴ ![]() ,得t=2.
,得t=2.
∴B1(2,0,0), ![]() ,
,
设平面AB1C的法向量为 ![]()
则 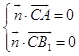 得x=y=z,取
得x=y=z,取 ![]() =(1,1,1)
=(1,1,1)
记直线BC与平面AB1C所成角为θ,且 ![]()
则 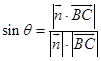 =
= ![]()
∴ ![]()
故直线BC与平面AB1C所成角的正切值为 ![]() .
.
【解析】(1)根据题目特点,可由证面面平行,得到线面平行.(2)方法一:找出线面所成角,再构造三角形求线面角的正切值;方法二:建立空间直角坐标系,根据向量所成角,求得线面角.
【考点精析】掌握直线与平面平行的判定和空间角的异面直线所成的角是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则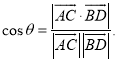 .
.

 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】若关于某设备的使用年限x(年)和所支出的维修费y(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系.
(1) 请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
![]() ;
;
(2) 估计使用年限为10年时,试求维修费用约是多少?(精确到两位小数)