题目内容
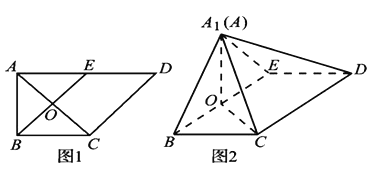
【题目】如图1,在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,E是AD的中点,O是AC与BE的交点.将
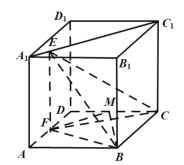
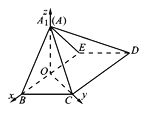
,E是AD的中点,O是AC与BE的交点.将![]() 沿BE折起到图2中
沿BE折起到图2中![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求平面
,求平面![]() 与平面
与平面![]() 夹角(锐角)的余弦值.
夹角(锐角)的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1) 因为![]() ,由
,由![]() ,可知
,可知![]() ,
,![]() .即证得
.即证得![]() 平面
平面![]() ,进而可得
,进而可得![]() 平面
平面![]() .
.
(2)合理建立坐标系,通过求出平面![]() 与平面
与平面![]() 的法向量
的法向量![]() ,利用公式
,利用公式![]() 即可求得.
即可求得.
解:(1)在图1中,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即在图2中,
,即在图2中,
![]() ,
,![]() .
.
又![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以![]() .
.
(2)由已知,![]() ,
,
又由(Ⅰ)知,![]() ,
,![]()
所以![]() 为二面角
为二面角![]() 的平面角,所以
的平面角,所以![]() .
.
如图,以O为原点,建立空间直角坐标系,
因为![]() ,
,![]() ,
,
所以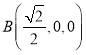 ,
,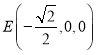 ,
,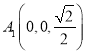
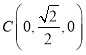 ,
,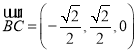 ,
,
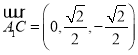 ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 与平面
与平面![]() 夹角为
夹角为![]() ,
,
由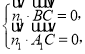 得
得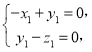 取
取![]() ,
,
由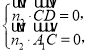 得
得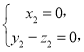 取
取![]() ,
,
从而![]() ,
,
即平面![]() 与平面
与平面![]() 夹角的余弦值为
夹角的余弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某家电公司进行关于消费档次的调查,根据家庭年均家电消费额将消费档次分为4组:不超过3000元、超过3000元且不超过5000元、超过5000元且不超过10000元、超过10000元,从A、B两市中各随机抽取100个家庭,统计数据如下表所示:
消费 档次 | 不超过3000元 | 超过3000元 且不超过5000元 | 超过5000元 且不超过10000元 | 超过10000元 |
A市 | 20 | 50 | 20 | 10 |
B市 | 50 | 30 | 10 | 10 |
年均家电消费额不超过5000元的家庭视为中低消费家庭,超过5000元的视为中高消费家庭.
(1)从A市的100个样本中任选一个家庭,求此家庭属于中低消费家庭的概率;
(2)现从A、B两市中各任选一个家庭,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
(3)以各消费档次的区间中点对应的数值为该档次的家庭年均家电消费额,估计A、B两市中,哪个市的家庭年均家电消费额的方差较大(直接写出结果,不必说明理由).