题目内容
16．某商场出售一种产品．每天可卖1000件，每件可获利40元．根据经验，若单价每降低1元，则每天可多卖100件，已知每件产品最高获利不超过40元．（1）求出总获利f（x）与每件的获利x之间的函数关系式，并写出定义域；
（2）每件获利应定为多少元时，总获利最大？并求最大获利为多少元？
分析 （1）通过设每件获利x元，利用总获利=单件利润×销售量，代入计算即得结论；
（2）通过（1）配方、即得结论．
解答 解：（1）设每件获利x元，其中0≤x≤40，
则每件降价（40-x）元，每天卖出商品件数为1000+100（40-x），
∴总获利f（x）=[1000+100（40-x）]x
=-100（x2-50x）
=-100（x-25）2+62500（0≤x≤40）；
（2）由（1）可知当x=25时，f（x）取最大值62500，
∴每件获利应定为25元时，总获利最大，且最大获利为62500元．
点评 本题考查函数模型的选择与应用，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
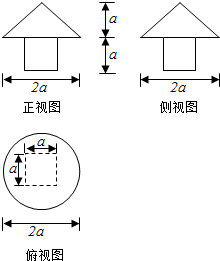一个几何体的三视图如图，则它的表面积为4a2+（1+$\sqrt{2}$）πa2，体积为a3+$\frac{1}{3}{πa}^{3}$．
已知正三棱锥V-ABC的正视图和俯视图如图所示，其中VA=4，AC=2$\sqrt{3}$，求该三棱锥的表面积．