题目内容
17.设x,y满足y=-x+1,则x2+y2的最小值为( )| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 利用基本不等式的变形得x2+y2≥$\frac{(x+y)^{2}}{2}$,问题得以解决.
解答 解:因为x,y满足y=-x+1,所以x+y=1,
因为x2+y2≥$\frac{(x+y)^{2}}{2}$=$\frac{1}{2}$,当且仅当x=y=$\frac{1}{2}$时取等号.
所以则x2+y2的最小值为$\frac{1}{2}$.
故选:C.
点评 本题主要考查基本不等式的运用,属于基础题.

练习册系列答案
相关题目
8.已知函数f(x)=x2+(m-2)x-5-m有两个小于2的零点,则实数m的取值范围( )
| A. | (5,+∞) | B. | (2,+∞) | C. | (-∞,2) | D. | (2,5) |
6.在棱长为1的正方体ABCD-A1B1C1D1中,BC与B1D间的距离是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\frac{\sqrt{5}}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
7.已知a<b<0,则下列不等式正确的是( )
| A. | a2<b2 | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | 2a<2b | D. | ab<b2 |
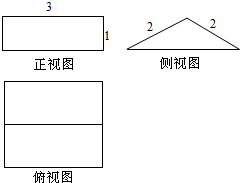 一个几何体的正视图是长为3、宽为1的矩形,侧视图是腰长为2的等腰三角形,则该几何的表面积为12+8$\sqrt{3}$.
一个几何体的正视图是长为3、宽为1的矩形,侧视图是腰长为2的等腰三角形,则该几何的表面积为12+8$\sqrt{3}$.