题目内容
设函数f (x) = a–|x| (a>0且a≠1)若f (2) = 4,则a = 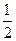 ,f (–2)与f (1)的大小关系是.
,f (–2)与f (1)的大小关系是.
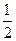 ,f (–2)与f (1)的大小关系是.
,f (–2)与f (1)的大小关系是.f (–2) >f (1)
由f (2) = a–2 = 4,解得a = 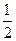 ,∴f (x) = 2|x|∴f (–2) = 4>2 = f (1).
,∴f (x) = 2|x|∴f (–2) = 4>2 = f (1).
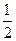 ,∴f (x) = 2|x|∴f (–2) = 4>2 = f (1).
,∴f (x) = 2|x|∴f (–2) = 4>2 = f (1).
练习册系列答案
相关题目
题目内容
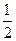 ,f (–2)与f (1)的大小关系是.
,f (–2)与f (1)的大小关系是.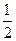 ,∴f (x) = 2|x|∴f (–2) = 4>2 = f (1).
,∴f (x) = 2|x|∴f (–2) = 4>2 = f (1).