题目内容
10.已知cosα=$\frac{1}{3}$,α∈(-$\frac{π}{2}$,0).(1)求cos($\frac{π}{3}$-α)和sin($\frac{π}{6}$+α)的值;
(2)如果钝角β的终边过点P(-2$\sqrt{2}$,1),求α+β的值.
分析 (1)由已知利用同角三角函数基本关系公式,可得sinα,结合两角差的余弦公式,及诱导公式可得答案;
(2)求出钝角β的三角函数值,求出α+β的余弦,可得答案.
解答 解:(1)∵cosα=$\frac{1}{3}$,α∈(-$\frac{π}{2}$,0).
∴sinα=-$\sqrt{1-(\frac{1}{3})^{2}}$=-$\frac{2\sqrt{2}}{3}$,
∴cos($\frac{π}{3}$-α)=cos$\frac{π}{3}$cosα+sin$\frac{π}{3}$sinα=$\frac{1}{2}$×$\frac{1}{3}$-$\frac{\sqrt{3}}{2}$×$\frac{2\sqrt{2}}{3}$=$\frac{1-2\sqrt{6}}{6}$,
sin($\frac{π}{6}$+α)=sin[$\frac{π}{2}$-($\frac{π}{3}$-α)]=cos($\frac{π}{3}$-α)=$\frac{1-2\sqrt{6}}{6}$,
(2)钝角β∈($\frac{π}{2}$,π),则α+β∈(0,π),
∵钝角β的终边过点P(-2$\sqrt{2}$,1),
∴r=3,
∴sinβ=$\frac{1}{3}$,cosβ=-$\frac{2\sqrt{2}}{3}$,
∴cos(α+β)=cosαcosβ-sinαsinβ=-$\frac{1}{3}$×$\frac{2\sqrt{2}}{3}$+$\frac{2\sqrt{2}}{3}$×$\frac{1}{3}$=0,
∴α+β=$\frac{π}{2}$.
点评 本题考查的知识点是同角三角函数基本关系公式,两角和与差的余弦公式,诱导公式,三角函数的定义,难度中档.

 在如图所示的韦恩图中,A,B是非空集合,定义A*B表示阴影部分集合,若集合A={x|y=$\sqrt{3x-{x}^{2}}$,x,y∈R},B={y|y=4x,x>0},则A*B=[0,1].
在如图所示的韦恩图中,A,B是非空集合,定义A*B表示阴影部分集合,若集合A={x|y=$\sqrt{3x-{x}^{2}}$,x,y∈R},B={y|y=4x,x>0},则A*B=[0,1].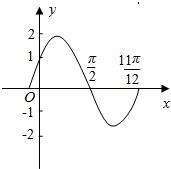 如图是函数y=2sin(ωx+φ)(|φ|<$\frac{π}{2}$)的图象.
如图是函数y=2sin(ωx+φ)(|φ|<$\frac{π}{2}$)的图象.