题目内容
2.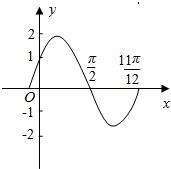 如图是函数y=2sin(ωx+φ)(|φ|<$\frac{π}{2}$)的图象.
如图是函数y=2sin(ωx+φ)(|φ|<$\frac{π}{2}$)的图象.(1)求ω、φ的值;
(2)求函数图象的对称轴方程.
分析 (1)由图象过(0,1)及|φ|<$\frac{π}{2}$,求出φ的值,函数图象过点($\frac{11π}{12}$,0),据五点法作图的过程知ω•$\frac{11π}{12}$+$\frac{π}{6}$=2π,求出ω.
(2)由2x+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z即可解得函数图象的对称轴方程.
解答 解:(1)因为函数图象过(0,1),所以,1=2sinφ,∴sinφ=$\frac{1}{2}$,∵|φ|<$\frac{π}{2}$,
∴φ=$\frac{π}{6}$,故函数y=2sin(ωx+$\frac{π}{6}$),又∵函数图象过点($\frac{11π}{12}$,0),
∴0=2sin(ω•$\frac{11π}{12}$+$\frac{π}{6}$),由五点法作图的过程知,ω•$\frac{11π}{12}$+$\frac{π}{6}$=2π,
∴ω=2,综上,φ=$\frac{π}{6}$,ω=2,
(2)∵由(1)可得函数解析式为:y=2sin(2x+$\frac{π}{6}$),
∴由2x+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z即可解得函数图象的对称轴方程为:x=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z.
点评 本题考查五点法作图的方法,在本题图中的一个完整的标准周期内,图象上的五个关键点的横坐标分别为:0,$\frac{π}{2}$,π,$\frac{3π}{2}$,2π,考查了正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
12.已知角α的终边经过点P(-1,0),则cosα的值为( )
| A. | 0 | B. | -1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
17.函数y=2cos(-4x+$\frac{π}{2}$)的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | 2π | D. | π |