题目内容
15.已知直线过点(1,1),则被圆x2+y2=4截得的弦长最大时的直线方程为x-y=0.分析 被圆截得的弦最长时的直线方程为过圆心的直线,由圆方程得到圆心坐标,确定出所求直线方程即可.
解答 解:圆x2+y2=4的圆心Q(0,0),
∵P(1,1),
∴被圆截得的弦最长时的直线PQ方程为y-1=1×(x-1),即x-y=0.
故答案为:x-y=0.
点评 此题考查了直线与圆相交的性质,以及圆的标准方程,根据题意得出过圆心的直线被圆截得的弦最长是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
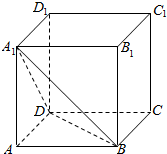 如图,在棱长为a的正方体ABCD-A1B1C1D1中,求A到平面A1BD的距离d.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,求A到平面A1BD的距离d.