题目内容
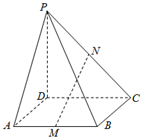 如图,四棱锥P-ABCD的底面是边长是1的正方形,侧棱PD⊥平面ABCD,M、N分别是AB、PC的中点.
如图,四棱锥P-ABCD的底面是边长是1的正方形,侧棱PD⊥平面ABCD,M、N分别是AB、PC的中点.(1)求证:MN∥平面PAD;
(2)记MN=x,V(x)表示四棱锥P-ABCD的体积,求V(x)的表达式(不必讨论x的取值范围).
分析:(1)取CD的中点E,连接ME、NE,由三角形中位定理,可得ME∥AD,NE∥PD,进而由面面平行的第二判定定理可得平面MNE∥平面PAD,进而由面面平行的性质得到MN∥平面PAD;
(2)由PD⊥平面ABCD,结合(1)中NE∥PD,可得NE⊥平面ABCD,进而NE⊥ME,由勾股定理可用x表示出NE,即
PD,代入棱锥体积公式可得答案.
(2)由PD⊥平面ABCD,结合(1)中NE∥PD,可得NE⊥平面ABCD,进而NE⊥ME,由勾股定理可用x表示出NE,即
| 1 |
| 2 |
解答: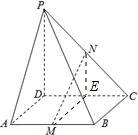 证明:(1)取CD的中点E,连接ME、NE,
证明:(1)取CD的中点E,连接ME、NE,
由M、N分别是AB、PC的中点
则ME∥AD,NE∥PD…(2分),
因为ME∩NE=E,ME,NE?平面MNE,AD,PD?平面PAD
所以平面MNE∥平面PAD…(4分),
又∵MN?平面MNE,
所以MN∥平面PAD…(6分).
解:(2)由(1)中NE∥PD,
又∵PD⊥平面ABCD,
所以NE⊥平面ABCD…(8分),
又∵ME?平面ABCD,
∴NE⊥ME…(9分),
∴MN2=ME2+NE2,
所以NE=
=
…(10分),
由(1)知PD=2NE=2
…(11分),
所以V(x)=
Sh=
×SABCD×PD…(13分),
=
…(14分).
 证明:(1)取CD的中点E,连接ME、NE,
证明:(1)取CD的中点E,连接ME、NE,由M、N分别是AB、PC的中点
则ME∥AD,NE∥PD…(2分),
因为ME∩NE=E,ME,NE?平面MNE,AD,PD?平面PAD
所以平面MNE∥平面PAD…(4分),
又∵MN?平面MNE,
所以MN∥平面PAD…(6分).
解:(2)由(1)中NE∥PD,
又∵PD⊥平面ABCD,
所以NE⊥平面ABCD…(8分),
又∵ME?平面ABCD,
∴NE⊥ME…(9分),
∴MN2=ME2+NE2,
所以NE=
| MN2-ME2 |
| x2-1 |
由(1)知PD=2NE=2
| x2-1 |
所以V(x)=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 2 |
| 3 |
| x2-1 |
点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,其中(1)的关键是熟练掌握线线平行,面面平行,线面平行之间的相互转化,(2)的关键是分别用x表示出棱锥的高和底面积.

练习册系列答案
相关题目

 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=