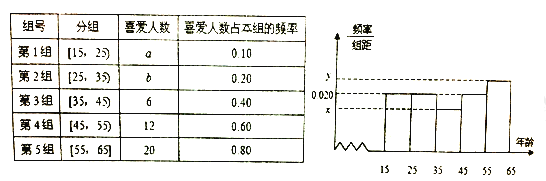
题目内容
【题目】如图所示,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F.
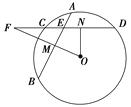
证明:(1)∠MEN+∠NOM=180°;
(2)FE·FN=FM·FO.
【答案】(1)见解析(2)见解析
【解析】试题分析:因为M,N分别是弦AB,CD的中点,所以OM⊥AB,ON⊥CD,又四边形的内角和等于360°,故∠MEN+∠NOM=180°;(2)O,M,E,N四点共圆,故由割线定理即得
FE·FN=FM·FO.
试题解析:
证明:(1)如图所示,

因为M,N分别是弦AB,CD的中点,所以OM⊥AB,
ON⊥CD,
即∠OME=90°,∠ENO=90°,
因此∠OME+∠ENO=180°.
又四边形的内角和等于360°,
故∠MEN+∠NOM=180°.
(2)由(1)知,O,M,E,N四点共圆,
故由割线定理即得
FE·FN=FM·FO.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目