题目内容
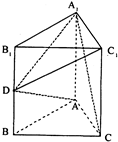 如图,直三棱柱ABC-A1B1C1,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点.
如图,直三棱柱ABC-A1B1C1,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点.(Ⅰ)求证:AD⊥平面A1DC;
(Ⅱ)求异面直线C1D与直线A1C所成角的余弦值.
分析:解法一:几何法
(I)根据直棱柱的几何特征,结合∠B1A1C1=90°,可证得A1C1⊥平面A1B1BA,进而AD⊥A1C1,由勾股定理可得A1D⊥AD,最后由线面垂直的判定定理得到AD⊥平面A1DC;
(Ⅱ)连结AC1交A1C于点E,取AD的中点F,连结EF,则EF∥C1D,∠CEF或它的补角就是异面直线C1D与直线A1C所成的角,解△CEF可得答案.
解法二:向量法
(I)以A为原点建立坐标系,求出
,
,
的坐标后,根据向量垂直的充要条件,及线面垂直的判定定理可得AD⊥平面A1DC;
(Ⅱ)求出直线C1D与直线A1C的方向向量,代入向量夹角公式,可得答案.
(I)根据直棱柱的几何特征,结合∠B1A1C1=90°,可证得A1C1⊥平面A1B1BA,进而AD⊥A1C1,由勾股定理可得A1D⊥AD,最后由线面垂直的判定定理得到AD⊥平面A1DC;
(Ⅱ)连结AC1交A1C于点E,取AD的中点F,连结EF,则EF∥C1D,∠CEF或它的补角就是异面直线C1D与直线A1C所成的角,解△CEF可得答案.
解法二:向量法
(I)以A为原点建立坐标系,求出
| A1D |
| AD |
| A1C1 |
(Ⅱ)求出直线C1D与直线A1C的方向向量,代入向量夹角公式,可得答案.
解答: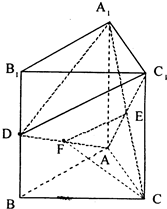 解法一:几何法
解法一:几何法
证明:(Ⅰ)∵AA1⊥平面A1B1C1,
∴AA1⊥A1C1
又A1C1⊥A1B1,
∴A1C1⊥平面A1B1BA
∴AD⊥A1C1
∵AD=
,A1D=
,AA1=2,
由ADAD2+A1D2=A
,
得A1D⊥AD
∵A1C1∩A1D=A1
∴AD⊥平面A1DC1…(7分)
解:(Ⅱ)连结AC1交A1C于点E,取AD的中点F,连结EF,则EF∥C1D
∴∠CEF或它的补角就是异面直线C1D与直线A1C所成的角
由(Ⅰ)知,AD⊥A1C1,则AD⊥AC,
又AF=
AD=
在△CEF中,CE=
A1C=
,EF=
C1D=
,CF=
=
cos∠CEF=
=
则异面直线C1D与直线A1C所成角的余弦值为
…(14分)
解法二:以A为原点建立坐标系,如图,则A1(0,0,2),C(0,1,0),C1(0,1,2)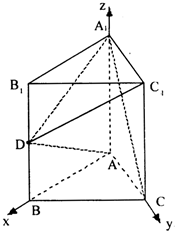
D(1,0,1)…(3分)
(Ⅰ)∵
=( 1,0,-1 ),
=( 1,0,1 ),
=( 0,1,0 ),
•
=1+0-1=0,
∴A1D⊥AD …(5分)
又
•
=0,∴AD⊥A1C1
∵A1D∩A1C1=A1
∴AD⊥A1DC1…(8分)
(Ⅱ)
=(1,-1,-1),
=(0,1,-2)
=
,
=
,
•
=1
cos<
,
>=
=
故直线C1D与直线A1C所成角的余弦值
…(14分)
 解法一:几何法
解法一:几何法证明:(Ⅰ)∵AA1⊥平面A1B1C1,
∴AA1⊥A1C1
又A1C1⊥A1B1,
∴A1C1⊥平面A1B1BA
∴AD⊥A1C1
∵AD=
| 2 |
| 2 |
由ADAD2+A1D2=A
| A | 2 1 |
得A1D⊥AD
∵A1C1∩A1D=A1
∴AD⊥平面A1DC1…(7分)
解:(Ⅱ)连结AC1交A1C于点E,取AD的中点F,连结EF,则EF∥C1D
∴∠CEF或它的补角就是异面直线C1D与直线A1C所成的角
由(Ⅰ)知,AD⊥A1C1,则AD⊥AC,
又AF=
| 1 |
| 2 |
| ||
| 2 |
在△CEF中,CE=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| AC2+AF2 |
| ||
| 2 |
cos∠CEF=
| CE2+EF2-CF2 |
| 2CE•EF |
| ||
| 15 |
则异面直线C1D与直线A1C所成角的余弦值为
| ||
| 15 |
解法二:以A为原点建立坐标系,如图,则A1(0,0,2),C(0,1,0),C1(0,1,2)

D(1,0,1)…(3分)
(Ⅰ)∵
| A1D |
| AD |
| A1C1 |
| A1D |
| AD |
∴A1D⊥AD …(5分)
又
| AD |
| A1C1 |
∵A1D∩A1C1=A1
∴AD⊥A1DC1…(8分)
(Ⅱ)
| C1D |
| A1C1 |
| |C1D| |
| 3 |
| |A1C| |
| 5 |
| C1D |
| A1C |
cos<
| C1D |
| A1C |
| ||||
|
| ||
| 15 |
故直线C1D与直线A1C所成角的余弦值
| ||
| 15 |
点评:本题考查的知识点是直线与平面垂直的判定,异面直线及其所成的角,解法一的关键是(1)熟练掌握线线垂直,线面垂直,面面垂直之间的相互转化,(2)将异面直线夹角转化为解三角形问题,解法二的关键是建立空间坐标系,将问题转化为向量夹角问题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.