题目内容

18．已知 f（x）是定义在R上的奇函数，当 x＜0时f（x）=log2（2-x），则f（0）+f（2）=-2．

分析 利用函数的解析式以及函数的奇偶性直接求解即可．

解答 解：f（x）是定义在R上的奇函数，当 x＜0时f（x）=log2（2-x），
则f（0）+f（2）=0-f（-2）=-log2（2+2）=-2，
故答案为：-2．

点评 本题考查函数的奇偶性的性质，函数的值的求法，考查计算能力．

练习册系列答案
相关题目
8．如图1，矩形ABCD中，|AB|=6，|BC|=2，E，F，G，H分别是矩形四条边的中点，分别以HF、EG所在直线为x轴，y轴建立平面直角坐标系，已知$\overrightarrow{OR}$=λ$\overrightarrow{OF}$，$\overrightarrow{CR′}$=λ$\overrightarrow{CF}$，其中0＜λ＜1
（1）求证：直线ER与GR′的交点M在椭圆Γ：$\frac{{x}^{2}}{9}$+y2=1上．
（2）如图2过点E作两条相互垂直的直线分别交椭圆Γ于点P，N（点P在y轴右侧）．求△EPN面积最大值及此时直线PE的方程．
9．在△ABC中，a，b，c分别为角A，B，C所对的边，已知b2+c2-a2=bc
（1）求角A的值；
（2）若a=$\sqrt{3}$，cosC=$\frac{\sqrt{3}}{3}$，求边c的长．
6．函数f（x）=sin（x+10°）+cos（x-20°）的最大值为$\sqrt{3}$．
13．直线3x-$\sqrt{3}$=0的倾斜角是（　　）
A．30°B．60°C．90°D．不存在
3．设函数f（x）=$\overrightarrow m$•$\overrightarrow n$，其中向量$\overrightarrow m$=（2cosx，1），$\overrightarrow n$=（cosx，$\sqrt{3}$sin2x），x∈R．
（1）求f（x）单调递减区间和图象的对称轴；
（2）在△ABC中，a、b、c分别是角A、B、C的对边，已知f（A）=2，求$\frac{b+c}{a}$的取值范围．
10．函数f（x）=e-x+lnx的导数为e-x+$\frac{1}{x}$．
7．独立性检验中的统计假设就是假设相关事件A，B（　　）
A．互斥B．不互斥C．相互独立D．不独立
8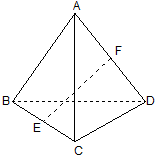．空间四边形ABCD中，若向量$\overrightarrow{AB}$=（-3，5，2），$\overrightarrow{CD}$=（-7，-1，-4）点E，F分别为线段BC，AD的中点，则$\overrightarrow{EF}$的坐标为（　　）
A．（2，3，3）B．（-2，-3，-3）C．（5，-2，1）D．（-5，2，-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网