题目内容
(本题满分20分,其中第1小题4分,第2小题6分,第3小题10分)
已知![]() 是直线
是直线![]() 上的
上的![]() 个不同的点(
个不同的点(![]() ,
,![]() 、
、![]() 均为非零常数),其中数列
均为非零常数),其中数列![]() 为等差数列.
为等差数列.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)若点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求证:
,求证: ![]() ;
;
(3) 设![]() ,且当
,且当![]() 时,恒有
时,恒有![]() (
(![]() 和
和![]() 都是不大于
都是不大于![]() 的正整数, 且
的正整数, 且![]() ).试探索:在直线
).试探索:在直线![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() 成立?请说明你的理由.
成立?请说明你的理由.
(本题满分20分,其中第1小题4分,第2小题6分,第3小题10分)
解:(1)证:设等差数列![]() 的公差为
的公差为![]() ,
,
因为![]() ,
,
所以![]() 为定值,即数列
为定值,即数列![]() 也成等差数列.
也成等差数列.
(2)证:因为点![]() 、
、![]() 和
和![]() 都是直线
都是直线![]() 上一点,故有
上一点,故有![]() (
(![]() )
)
于是,![]()
![]()
![]()
令![]() ,
,![]() ,则有
,则有![]() .
.
(3)(文科)假设存在点![]() 满足要求
满足要求![]() ,
,
则有![]() ,
,
又当![]() 时,恒有
时,恒有![]() ,则又有
,则又有
![]() ,
,
所以![]()
又因为数列![]() 成等差数列,
成等差数列,
于是![]() ,
,
所以,![]()
故![]() ,同理
,同理![]() ,且点
,且点![]() 在直线上(是
在直线上(是![]() 、
、![]() 的中点),即存在点
的中点),即存在点![]() 满足要求.
满足要求.
(3)(理科)
提出命题:(在本题大前提下)若点![]() 满足
满足![]() ,则系数数列的和
,则系数数列的和![]() 是点
是点![]() 在直线
在直线![]() 上的充要条件.
上的充要条件.
证明:设![]() ,由条件
,由条件![]() ,
,
先证充分性:“当![]() 时,点
时,点![]() 在直线
在直线![]() 上”.
上”.
因为![]() ,
,
故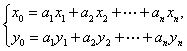
而![]() (
(![]() ),所以
),所以
![]()
![]()
![]()
当![]() 时,即有
时,即有![]() ,即点
,即点![]() 在直线
在直线![]() 上.
上.
再证必要性:“若点![]() 在直线
在直线![]() 上,则
上,则![]() .”
.”
因为![]() ,
,
故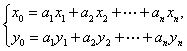
而因为![]() (
(![]() ),所以
),所以
![]()
![]()
![]()
又因为点![]() 在直线
在直线![]() 上,所以满足
上,所以满足![]() ,故
,故![]() .
.
补充:由以上证明进一步可知,对于直线![]() 上任一点
上任一点![]() ,若满足
,若满足![]() ,则都有
,则都有![]() .
.

(本题满分12分)
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频 数 | 40 | 20 |
| 10 |
|
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如右表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元. 用![]() 表示经销一辆汽车的利润.(1)求上表中的
表示经销一辆汽车的利润.(1)求上表中的![]() 值;(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率
值;(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率![]() ;(3)求
;(3)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
(本题满分14分,第1小题满分7分,第2小题满分7分)
为了研究某种癌细胞的繁殖规律和一种新型抗癌药物的作用,将癌细胞注入一只小白鼠体内进行实验,经检测,癌细胞的繁殖规律与天数的关系如下表.已知这种癌细胞在小白鼠体内的个数超过 时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的
时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的 .
.
|
天数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
… |
|
癌细胞个数 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
… |
(1)要使小白鼠在实验中不死亡,第一次最迟应在第几天注射该种药物?(精确到1天)
(2)若在第10天,第20天,第30天,……给小白鼠注射这种药物,问第38天小白鼠是否仍然存活?请说明理由.
(本题满分12分)某电视生产厂家今年推出A、B、C、D四种款式电视机,每种款式电视机的外观均有黑色、银白色两种。四月份的电视机产量如下表(单位:台)
|
|
款式A |
款式B |
款式C |
款式D |
|
黑色 |
150 |
200 |
200 |
|
|
银白色 |
160 |
180 |
200 |
150 |
若按电视机的款式采取分层抽样的方法在这个月生产的电视机中抽取70台,其中有C种款式的电视机20台。
(1) 求 的值;
的值;
(2) 若在C款式电视机中按颜色进行分层抽样抽取一个容量为6的样本,然后将该样本看成一个总体,从中任取2台,求恰有1台黑色、1台银白色电视的概率;
(3) 用简单随机抽样的方法从A种款式电视机中抽取10台,对其进行检测,它们的得分如下:94,92,92,96,97,95,98,90,94,97。如果把这10台电视机的得分看作一个样本,从中任取一个数,求该数与样本平均数之差的绝对值不超过2的概率。


 为定义域为
为定义域为 的函数,对任意
的函数,对任意 ,都满足:
,都满足: ,
, ,且当
,且当 时,
时,
 上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;
上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论; 上的解析式.
上的解析式.