题目内容
(1)已知α、β是方程x2＋(2m－1)x＋4－2m＝0的两个实根，且α<2<β，求m的取值范围；(2)若方程x2＋ax＋2＝0的两根都小于－1，求a的取值范围．
（1）m<－3（2）2
≤a<3
≤a<3(1)设f(x)＝x2＋(2m－1)x＋4－2m.
∵α、β是方程f(x)＝0的两个根，且α<2<β，
∴f(2)<0，即22＋2(2m－1)＋4－2m<0，得m<－3.
(2)设f(x)＝x2＋ax＋2,f(－1)＝1－a＋2，Δ＝a2－8.由题意，得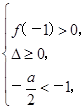
∴2≤a<3
∵α、β是方程f(x)＝0的两个根，且α<2<β，
∴f(2)<0，即22＋2(2m－1)＋4－2m<0，得m<－3.
(2)设f(x)＝x2＋ax＋2,f(－1)＝1－a＋2，Δ＝a2－8.由题意，得
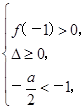∴2≤a<3
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
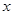吨，运费为4万元/次，一年的总存储费用为
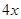万元，要使一年的总运费与总存储费用之和最小，则
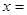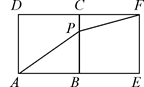
___ ____ 吨．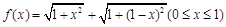
的性质，构造了如图所示的两个边长为
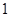的正方形
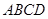和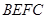
，点P是边BC上的一个动点，设CP=x，则
．
；
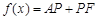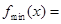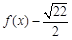的零点个数是.
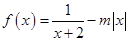有三个零点，则实数
的取值范围为 ．
,用二分法求方程
内近似解的过程中得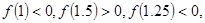
则方程的根落在区间（ ）
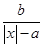(a>0，b>0)的函数因其图象类似于汉字中的“囧”字，故生动地称为“囧函数”，若当a＝1，b＝1时的“囧函数”与函数y＝lg|x|的交点个数为n，则n＝________.
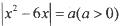的解集为P，则P中所有元素的和可能是（ ）