题目内容
数列{an}的前n项和为Sn,若a1=1,an+1 =3Sn(n ≥1),则a6=
| A.3 ×44 | B.3 ×44+1 | C.44 | D.44+1 |
答案:A
解析:由an+1 =3Sn,得an =3Sn-1(n ≥ 2),相减得an+1-an =3(Sn-Sn-1)= 3an,则an+1=4an(n ≥ 2),a1=1,a2=3,则a6= a2·44=3×44,选A.
解析:由an+1 =3Sn,得an =3Sn-1(n ≥ 2),相减得an+1-an =3(Sn-Sn-1)= 3an,则an+1=4an(n ≥ 2),a1=1,a2=3,则a6= a2·44=3×44,选A.
分析:根据已知的an+1=3Sn,当n大于等于2时得到an=3Sn-1,两者相减,根据Sn-Sn-1=an,得到数列的第n+1项等于第n项的4倍(n大于等于2),所以得到此数列除去第1项,从第2项开始,为首项是第2项,公比为4的等比数列,由a1=1,an+1=3Sn,令n=1,即可求出第2项的值,写出2项以后各项的通项公式,把n=6代入通项公式即可求出第6项的值.
解:由an+1=3Sn,得到an=3Sn-1(n≥2),
两式相减得:an+1-an=3(Sn-Sn-1)=3an,
则an+1=4an(n≥2),又a1=1,a2=3S1=3a1=3,
得到此数列除去第一项后,为首项是3,公比为4的等比数列,
所以an=a2qn-2=3×4n-2(n≥2)
则a6=3×44.
故选A

练习册系列答案
相关题目
 的前n项和,
的前n项和,  .(I)求数列
.(I)求数列 的值.
的值.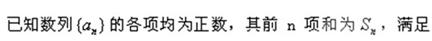

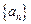 满足
满足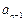 +
+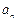 =4n-3(n∈
=4n-3(n∈ ).
). =2,求数列
=2,求数列 ;
;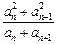 ≥5成立,求
≥5成立,求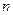 为偶数时,
为偶数时, 的通项公式;
的通项公式; ,且A、B、C
,且A、B、C .101 C.200 D.201
.101 C.200 D.201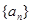 中,若
中,若 ,
,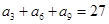 ,则前9项的和
,则前9项的和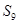 等于
等于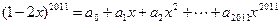 则
则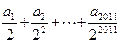 的值为( ▲ )
的值为( ▲ ) 2
2  0
0

 称为数列{an}的“均和”.现有一个共2010项的数列{an}:a1,a2,a3,…,a2009,a2010若其“均和”为2011,则有2011项的数列1,a1,a2,a3,…,a2009,a2010的“均和”为 .
称为数列{an}的“均和”.现有一个共2010项的数列{an}:a1,a2,a3,…,a2009,a2010若其“均和”为2011,则有2011项的数列1,a1,a2,a3,…,a2009,a2010的“均和”为 .