题目内容
下列命题中:①若p、q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件;
②若p为:?x∈R,x2+2x+2≤0,则¬p为:?x∈R,x2+2x+2>0;
③若命题“?x∈R,x2+(a-1)x+1<0”是假命题,则实数a的取值范围是-1≤a≤3;
④已知命题p:?x∈R,使tanx=1,命题q:x2-3x+2<0的解集是{x|1<x<2},则命题“¬p∨¬q”是假命题.所有正确命题的序号是 .
【答案】分析:利用常用逻辑用语中的基本知识进行甄别和判断是解决本题的关键,要理解充要条件的判断、含有一个量词命题否定的正确表述、复合命题真假的判断.
解答:解:①“p且q为真”可以得出p,q均真,故“p或q为真”,反之“p或q为真”不一定有“p且q为真”,故“p且q为真”是“p或q为真”的充分不必要条件,而不是必要不充分条件,故①错误;
根据特称命题的否定的叙述方法,可知②正确;
命题“?x∈R,x2+(a-1)x+1<0”是假命题?命题“?x∈R,x2+(a-1)x+1≥0”是真命题?(a-1)2-4≤0?-1≤a≤3,故③正确;
命题p:?x∈R,使tanx=1是正确的,命题q:x2-3x+2<0的解集是{x|1<x<2}也是正确的,故非p、非q均为假命题,因此“¬p∨¬q”是假命题,故④正确.
故答案为:②③④.
点评:本题考查常用逻辑用语的基本知识,要把握好充要条件的判断,含有一个量词的命题的否定的叙述、复合命题真假与简单命题之间的关系,属于基本题型.
解答:解:①“p且q为真”可以得出p,q均真,故“p或q为真”,反之“p或q为真”不一定有“p且q为真”,故“p且q为真”是“p或q为真”的充分不必要条件,而不是必要不充分条件,故①错误;
根据特称命题的否定的叙述方法,可知②正确;
命题“?x∈R,x2+(a-1)x+1<0”是假命题?命题“?x∈R,x2+(a-1)x+1≥0”是真命题?(a-1)2-4≤0?-1≤a≤3,故③正确;
命题p:?x∈R,使tanx=1是正确的,命题q:x2-3x+2<0的解集是{x|1<x<2}也是正确的,故非p、非q均为假命题,因此“¬p∨¬q”是假命题,故④正确.
故答案为:②③④.
点评:本题考查常用逻辑用语的基本知识,要把握好充要条件的判断,含有一个量词的命题的否定的叙述、复合命题真假与简单命题之间的关系,属于基本题型.

练习册系列答案
相关题目
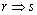 B.p:
B.p: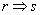 q:
q: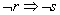
 q:
q:  D. p:
D. p: q:
q: