Question

【题目】已知抛物线的焦点为,直线与轴交点为,与的交点为,且．

（Ⅰ）求的方程;

（Ⅱ）过的直线与相交于两点,若的垂直平分线与相交于两点,且四点在同一圆上,求的方程．

Answer 1

【答案】（Ⅰ）（Ⅱ）或

【解析】

试题分析：（Ⅰ）设点Q的坐标为（，4），把点Q的坐标代入抛物线C的方程，求得，根据求得 p的值，可得C的方程．（Ⅱ）设l的方程为 x=my+1 （m≠0），代入抛物线方程化简，利用韦达定理、中点公式、弦长公式求得弦长|AB|．把直线l′的方程代入抛物线方程化简，利用韦达定理、弦长公式求得|MN|．由于MN垂直平分线段AB，故AMBN四点共圆等价于|AE|=|BE|=|MN|，由此求得m的值，可得直线l的方程

试题解析：（Ⅰ）设点,,则由抛物线定义知,

所以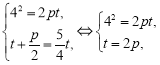得,即的方程为;

（Ⅱ）如右图所示,设,

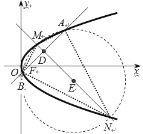
中点为,,则由

得,其中恒成立,

所以,

,

易求得,又,

所以,,即,

代入中得,,其中恒成立,

故,,

又易求得的中点,

故,而由共圆知,

,即,代入得

,同时约去且化简得

,又,所以,即,也即直线或．