题目内容
 (2007•肇庆二模)如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形.
(2007•肇庆二模)如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形.(Ⅰ)画出这个几何体的直观图;
(Ⅱ)若等腰直角三角形的直角边的长为a,求这个几何体的体积.
分析:(Ⅰ)这个几何体是一个底面与两个侧面都是等腰直角三角形的三棱锥,直观图如图.
(Ⅱ)由三视图可知三条侧棱相互垂直,根据体积公式易求.
(Ⅱ)由三视图可知三条侧棱相互垂直,根据体积公式易求.
解答: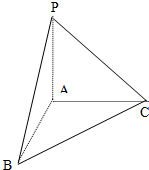 解:(Ⅰ)这个几何体是一个底面与两个侧面都是等腰直角三角形的
解:(Ⅰ)这个几何体是一个底面与两个侧面都是等腰直角三角形的
三棱锥,直观图如图.
(6分)
(Ⅱ)由三视图可得PA⊥AB,PA⊥AC.
又AB∩AC=A,∴PA⊥面ABC.(8分)
△ABC是等腰直角三角形,且AB=AC=a,
∴S△ABC=
a2.(10分)
∴VP-ABC=
PA•S△ABC=
a3.(12分)
 解:(Ⅰ)这个几何体是一个底面与两个侧面都是等腰直角三角形的
解:(Ⅰ)这个几何体是一个底面与两个侧面都是等腰直角三角形的三棱锥,直观图如图.
(6分)
(Ⅱ)由三视图可得PA⊥AB,PA⊥AC.
又AB∩AC=A,∴PA⊥面ABC.(8分)
△ABC是等腰直角三角形,且AB=AC=a,
∴S△ABC=
| 1 |
| 2 |
∴VP-ABC=
| 1 |
| 3 |
| 1 |
| 6 |
点评:本题考查由三视图与直观图的相互转化,求组合体的体积,考查空间想象能力,计算能力,是基础题.

练习册系列答案
相关题目