题目内容
平面α的斜线AB交α于点B,过定点A的动直线l与AB垂直,且交α于点C,则动点C的轨迹是
A.一条直线 B.一个圆 C.一个椭圆 D.双曲线的一支.
A
A
A.一条直线 B.一个圆 C.一个椭圆 D.双曲线的一支.
分析:由过定点A的动直线l与AB垂直,考虑l确定的面β与AB的垂直,由过平面外一点有且只有一个平面与已知直线垂直可知过定点A与AB垂直所有直线都在这个平面内,则直线l交α于点C转化为β与α的相交于一条直线,则问题解决.
解答:解:如图,设l与l′是其中的两条任意的直线,
则这两条直线确定一个平面β,且α的斜线AB⊥β,
由过平面外一点有且只有一个平面与已知直线垂直可知过定点A与AB垂直所有直线都在这个平面内,
故动点C都在平面β与平面α的交线上,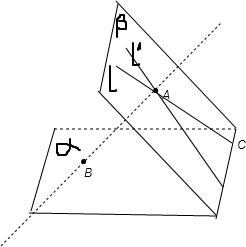
故选A
则这两条直线确定一个平面β,且α的斜线AB⊥β,
由过平面外一点有且只有一个平面与已知直线垂直可知过定点A与AB垂直所有直线都在这个平面内,
故动点C都在平面β与平面α的交线上,

故选A
点评:本题的考点是轨迹方程,主要考查轨迹与立体几何的交汇,考查线面垂直的判定、面面的相交,同时考查空间想象能力.有较强的综合性.

练习册系列答案
相关题目