题目内容
已知曲线C的方程为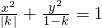 ,则当C为双曲线时,k的取值范围是________;当C为焦点在y轴上的椭圆时,k的取值范围是________.
,则当C为双曲线时,k的取值范围是________;当C为焦点在y轴上的椭圆时,k的取值范围是________.
(1,+∞) 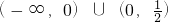
分析:(1)根据曲线是椭圆时的双曲线的方程的特点是方程中y2的分母和x2分母异号,列出不等式组,求出k的范围.
(2)要使曲线是为焦点在y轴上的椭圆,方程中y2的分母1-k大于x2分母|k|,且都大于0,列出不等式组,求出k的范围.
解答:(1)曲线为双曲线?|k|(1-k)<0
? 或
或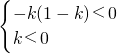
?k>1.即k的取值范围是(1,+∞).
(2)曲线为焦点在y轴上的椭圆?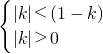
? 或
或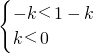
?k<0或0<k< .
.
故答案为:(1,+∞),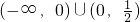 .
.
点评:解决椭圆的方程,注意焦点的位置在哪个坐标轴上,方程中哪个字母的分母就大.本题还考查了双曲线的标准方程.属基础题.
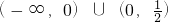
分析:(1)根据曲线是椭圆时的双曲线的方程的特点是方程中y2的分母和x2分母异号,列出不等式组,求出k的范围.
(2)要使曲线是为焦点在y轴上的椭圆,方程中y2的分母1-k大于x2分母|k|,且都大于0,列出不等式组,求出k的范围.
解答:(1)曲线为双曲线?|k|(1-k)<0
?
 或
或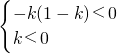
?k>1.即k的取值范围是(1,+∞).
(2)曲线为焦点在y轴上的椭圆?
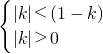
?
 或
或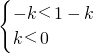
?k<0或0<k<
 .
.故答案为:(1,+∞),
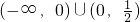 .
.点评:解决椭圆的方程,注意焦点的位置在哪个坐标轴上,方程中哪个字母的分母就大.本题还考查了双曲线的标准方程.属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目