题目内容
(2012•松江区三模)已知曲线C的方程为:x2+y2-2|x|-2|y|=0,P1、P2是曲线C上的两个点,则|P1P2|的最大值为( )
分析:利用绝对值的几何意义可知曲线C的图形,进而可得|P1P2|的最大值为一、三(或二、四)象限的圆的圆心距加上2个半径的长.
解答:解:利用绝对值的几何意义可知曲线C表示x2+y2-2x-2y=0,x2+y2+2x|-2y=0,x2+y2+2x+2y=0,x2+y2-2x+2y=0,分别在各个象限的部分(包括与坐标轴的交点)
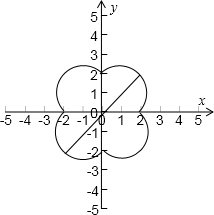
∵P1、P2是曲线C上的两个点,
∴|P1P2|的最大值为一、三(或二、四)象限的圆的圆心距加上2个半径的长
∴|P1P2|的最大值为2
+
+
=4
故选D.

∵P1、P2是曲线C上的两个点,
∴|P1P2|的最大值为一、三(或二、四)象限的圆的圆心距加上2个半径的长
∴|P1P2|的最大值为2
| 2 |
| 2 |
| 2 |
| 2 |
故选D.
点评:本题考查圆的方程,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 (2012•松江区三模)如图放置的边长为1的正方形ABCD的顶点A、D分别在x轴、y轴正半轴上(含原点)上滑动,则
(2012•松江区三模)如图放置的边长为1的正方形ABCD的顶点A、D分别在x轴、y轴正半轴上(含原点)上滑动,则