题目内容
如果椭圆的对称轴为坐标轴,短轴的一个端点与两焦点组成一正三角形,焦点在y轴上,且a-c=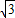 那么椭圆的方程是 .
那么椭圆的方程是 .
【答案】分析:根据短轴的一个端点与两焦点组成一正三角形,焦点在y轴上知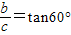 在结合a-c=
在结合a-c=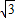 与a2=b2+c2求出a,b,c即可
与a2=b2+c2求出a,b,c即可
解答:解:由题意可设椭圆方程为: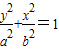
∵短轴的一个端点与两焦点组成一正三角形,焦点在y轴上
∴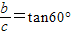
又∵a-c=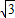 ,a2=b2+c2
,a2=b2+c2
∴a2=12,b2=9
∴椭圆的方程为: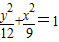
故答案为: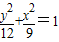
点评:本题考查了椭圆的标准方程,解三角形以及解方程组的相关知识,属于基础题.
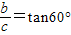 在结合a-c=
在结合a-c=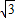 与a2=b2+c2求出a,b,c即可
与a2=b2+c2求出a,b,c即可解答:解:由题意可设椭圆方程为:
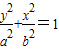
∵短轴的一个端点与两焦点组成一正三角形,焦点在y轴上
∴
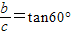
又∵a-c=
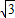 ,a2=b2+c2
,a2=b2+c2∴a2=12,b2=9
∴椭圆的方程为:
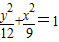
故答案为:
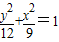
点评:本题考查了椭圆的标准方程,解三角形以及解方程组的相关知识,属于基础题.

练习册系列答案
相关题目
 那么椭圆的方程是 .
那么椭圆的方程是 . 那么椭圆的方程是 .
那么椭圆的方程是 .