题目内容
7.已知正数a、b、c满足a+b+c=1,则$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$的最小值是$\frac{9}{2}$.分析 由题意可得$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$=$\frac{1}{2}$[(a+b)+(b+c)+(c+a)]($\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$),再由三元基本不等式,即可得到最小值.
解答 解:由正数a、b、c满足a+b+c=1,
可得2=(a+b)+(b+c)+(c+a),
即有$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$=$\frac{1}{2}$[(a+b)+(b+c)+(c+a)]($\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$)
≥$\frac{1}{2}$•3$\root{3}{(a+b)(b+c)(c+a)}$•3$\root{3}{\frac{1}{a+b}•\frac{1}{b+c}•\frac{1}{c+a}}$=$\frac{9}{2}$,
当且仅当a=b=c=$\frac{1}{3}$时,取得最小值$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查基本不等式的运用:求最值,考查乘1法和化简运算能力,属于中档题.

练习册系列答案
相关题目
17.在数列{an}中,a1=cosθ,an+1=ansinθ,其中0<θ<2π,θ≠$\frac{π}{2}$且θ≠$\frac{3π}{2}$,若$\underset{lim}{n→∞}$(a1+a2+…+an)=$-\frac{\sqrt{3}}{3}$,则θ等于( )
| A. | $\frac{7π}{10}$ | B. | $\frac{5π}{12}$ | C. | $\frac{7π}{6}$ | D. | $\frac{5π}{6}$ |
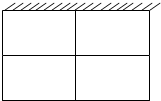 如图所示,某畜牧基地要围成相同面积的羊圈4间,一面可利用原有的墙壁,其余各面用篱笆围成,篱笆总长为36m,则每间羊圈的长和宽各为多少时,羊圈面积最大?
如图所示,某畜牧基地要围成相同面积的羊圈4间,一面可利用原有的墙壁,其余各面用篱笆围成,篱笆总长为36m,则每间羊圈的长和宽各为多少时,羊圈面积最大?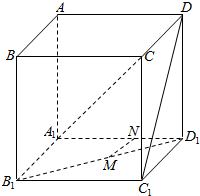 在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.
在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.