题目内容
7.对于定义在R上的奇函数f(x),满足f(-x)+f(3+x)=0,若f(-1)=1,则f(1)+f(2)+f(3)+…+f(2015)=( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 利用函数的奇偶性,以及函数的关系式,求出函数的周期,然后求解函数值即可.
解答 解:定义在R上的奇函数f(x),满足f(-x)+f(3+x)=0,
可得f(x)=f(3+x),所以函数的周期为3.
定义在R上的奇函数f(x),可知f(0)=0,
又f(-1)=1,
∴f(2)=f(-1)=1,f(1)=-f(-1)=-1.
f(1)+f(2)+f(3)=-1+1+0=0;
∴f(1)+f(2)+f(3)+…+f(2015)=671(f(1)+f(2)+f(3))+f(1)+f(2)=0-1+1=0.
故选:B.
点评 本题考查抽象函数的应用,函数的周期以及函数的奇偶性的应用,考查计算能力.

练习册系列答案
相关题目
19.下列命题正确的是( )
| A. | 垂直于同一条直线的两条直线平行 | B. | 垂直于同一个平面的两条直线平行 | ||
| C. | 平行于同一个平面的两条直线平行 | D. | 平行于同一条直线的两个平面平行 |
17.甲、乙两人约定在7:00~8:00之间在某处会面,且他们在这一时间段内任一时刻到达该处的可能性均相等,则他们中先到者等待的时间不超过15分钟的概率是( )
| A. | $\frac{9}{16}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{16}$ | D. | $\frac{5}{16}$ |
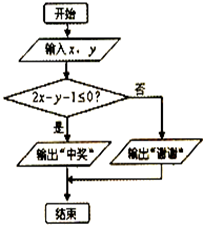 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.