题目内容
(本小题满分12分)已知函数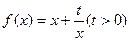 和点
和点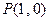 ,过点
,过点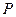 作曲线
作曲线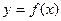 的两条切线
的两条切线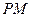 、
、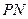 ,切点分别为
,切点分别为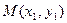 、
、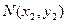 .
.
(1)求证: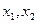 为关于
为关于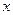 的方程
的方程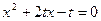 的两根;
的两根;
(2)设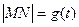 ,求函数
,求函数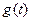 的表达式;
的表达式;
(3)在(2)的条件下,若在区间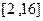 内总存在
内总存在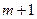 个实数
个实数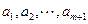 (可以相同),使得不等式
(可以相同),使得不等式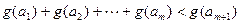 成立,求
成立,求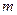 的最大值.
的最大值.
解:(1)由题意可知: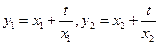
∵ 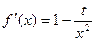 , ……………………………2分
, ……………………………2分
∴切线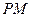 的方程为:
的方程为: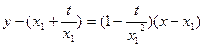 ,
,
又 切线
切线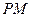 过点
过点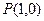 ,
, 有
有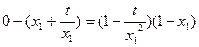 ,
,
即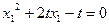 , ①
, ①
同理,由切线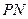 也过点
也过点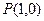 ,得
,得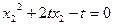 .②
.②
由①、②,可得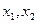 是方程
是方程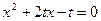 ( * )的两根……………………………4分
( * )的两根……………………………4分
(2)由( * )知.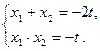
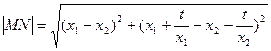
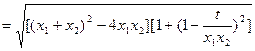
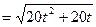 ,
,
∴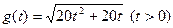 .……………………………8分
.……………………………8分
(3)易知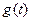 在区间
在区间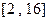 上为增函数,
上为增函数,
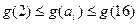
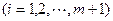 ,
,
则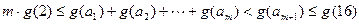 .……………………10分
.……………………10分
即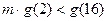 ,即
,即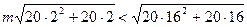 ,
,
所以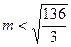 ,由于
,由于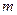 为正整数,所以
为正整数,所以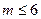 .
.
又当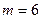 时,存在
时,存在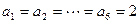 ,
,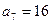 满足条件,
满足条件,
所以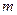 的最大值为
的最大值为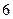 . …………12分
. …………12分
解析

练习册系列答案
相关题目
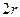 ,短半轴长为
,短半轴长为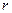 ,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记
,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记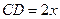 ,梯形面积为S.
,梯形面积为S. 求面积S以
求面积S以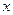 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;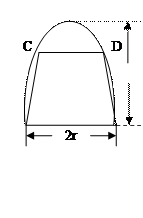

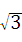 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0). 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;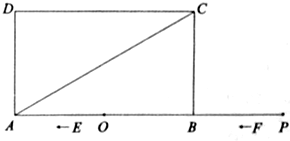
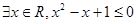 ;
; ),P(X≤6)=0.72,则P(X≤0)=0.28;
),P(X≤6)=0.72,则P(X≤0)=0.28; 的展开式的各项系数和为32,则展开式中x项的系数为20;
的展开式的各项系数和为32,则展开式中x项的系数为20;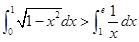
 为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg,针对这种销售情况,
为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg,针对这种销售情况, 为y元,求y与x的函数关系式;
为y元,求y与x的函数关系式; 上的函数
上的函数 同时满足下列三个条件:
同时满足下列三个条件: 均有
均有 成立;
成立;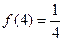 ;
; 时,都有
时,都有 成立。
成立。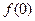 ,
, 的值;
的值; 的不等式
的不等式 .
.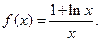
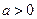 ,若函数在区间
,若函数在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围; 时,不等式
时,不等式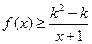 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。