题目内容
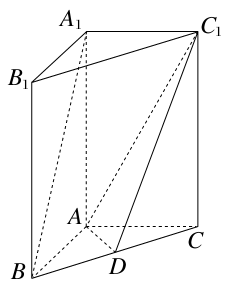
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,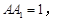
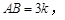
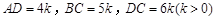 .
.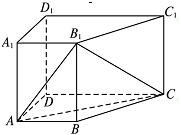
(Ⅰ)求证:CD⊥平面ADD1A1;
(Ⅱ)若直线AA1与平面AB1C所成角的正弦值为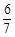 ,求k的值.
,求k的值.
(Ⅰ)见解析(Ⅱ)1
解析试题分析:(Ⅰ)取CD的中点为E,连结BE,则ADEB为平行四边形,所以AD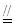 BE=4k,所以BC2=BE2+EC2,所以BE⊥DC,所以AD与BC垂直,AA1⊥面ABCD,所以AA1⊥CD,所以CD垂直面AA1D1D;(Ⅱ)以D为原点,DA,DC,DD1为
BE=4k,所以BC2=BE2+EC2,所以BE⊥DC,所以AD与BC垂直,AA1⊥面ABCD,所以AA1⊥CD,所以CD垂直面AA1D1D;(Ⅱ)以D为原点,DA,DC,DD1为 轴,建立空间直角坐标系,写出A、A1,B1,C的坐标,求出面AB1C的一个法向量,算出向量
轴,建立空间直角坐标系,写出A、A1,B1,C的坐标,求出面AB1C的一个法向量,算出向量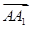 坐标,计算出这两个向量的夹角,再利用向量夹角与线面角关系,列出关于k的方程,若能解出k值..
坐标,计算出这两个向量的夹角,再利用向量夹角与线面角关系,列出关于k的方程,若能解出k值..
试题解析:(Ⅰ)取CD的中点E,连结BE.
∵AB∥DE,AB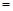 DE
DE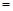 3k,∴四边形ABED为平行四边形, 2分
3k,∴四边形ABED为平行四边形, 2分
∴BE∥AD且BE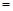 AD
AD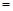 4k.
4k.
在△BCE中,∵BE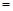 4k,CE
4k,CE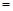 3k,BC
3k,BC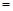 5k,∴BE2+CE2
5k,∴BE2+CE2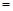 BC2,
BC2,
∴∠BEC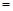 90°,即BE⊥CD,
90°,即BE⊥CD,
又∵BE∥AD,∴CD⊥AD. 4分
∵AA1⊥平面ABCD,CD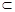 平面ABCD,
平面ABCD,
∴AA1⊥CD.又AA1∩AD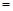 A,
A,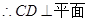 ADD1A1. 6分
ADD1A1. 6分
(Ⅱ)以D为原点,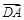 ,
,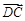 ,
,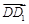 的方向为x,y,z轴的正方向建立如图所示的空间直角坐标系,
的方向为x,y,z轴的正方向建立如图所示的空间直角坐标系,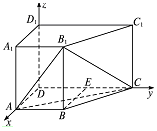
则
所以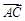
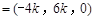 ,
,
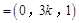 ,
,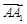
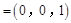 .
.
设平面AB1C的法向量n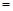 (x,y,z),
(x,y,z),
则由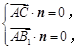 得
得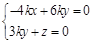
取y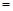 2,得
2,得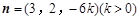 . 9分
. 9分
设AA1与平面AB1C所成角为θ,则
sin θ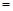 |cos〈
|cos〈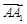 ,n〉|
,n〉|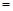

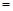
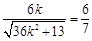 ,
,
解得k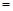 1,故所求k的值为1. 12分
1,故所求k的值为1. 12分
考点:面面垂直的性质,线面垂直的判定,线面角的计算,推理论证能力,运算求解能力,空间想象能力

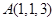 与点
与点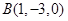 的距离为_____.
的距离为_____. ,则点
,则点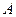 关于
关于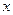 轴对称的点的坐标为 。
轴对称的点的坐标为 。 为矩形,
为矩形,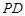 ⊥平面
⊥平面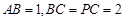 ,作如图3折叠,折痕
,作如图3折叠,折痕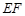
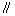
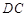 ,其中点
,其中点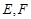 分别在线段
分别在线段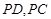 上,沿
上,沿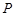 叠在线段
叠在线段 上的点记为
上的点记为 ,并且
,并且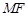 ⊥
⊥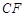 .(1)证明:
.(1)证明: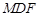 ;
;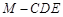 的体积.
的体积.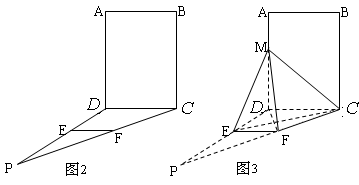
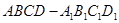 中,
中,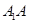
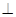 底面
底面 .四边形
.四边形 ,且
,且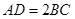 .过
.过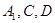 三点的平面记为
三点的平面记为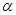 ,
,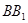 与
与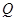 .
.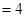 ,
,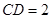 ,梯形
,梯形
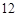 的正方形
的正方形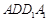 中,点
中,点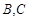 在线段
在线段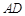 上,且
上,且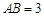 ,
,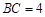 ,作
,作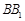 //
//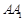 ,分别交
,分别交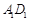 ,
,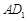 于点
于点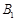 ,
,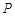 ,作
,作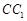 //
//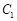 ,
,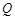 ,将该正方形沿
,将该正方形沿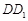 与
与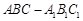 .
.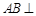 平面
平面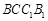 ;
; 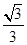 ,求|BE|的最小值.
,求|BE|的最小值.
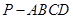 的底面的菱形,
的底面的菱形,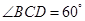 ,点
,点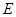 是
是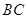 边的中点,
边的中点,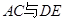 交于点
交于点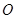 ,
,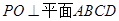
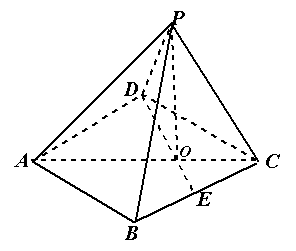
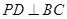 ;
; 的大小;
的大小;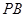 与
与 所成角的余弦值。
所成角的余弦值。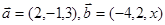 ,若
,若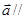
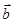 则
则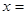 ______。
______。