题目内容
15.已知函数f(x)=(m-1)x2+2mx+3为偶函数,则f(x)的单调递增区间为(-∞,0).分析 f(x)=(m-1)x2+2mx+3若为偶函数,则表达式中显然不能含有一次项2mx,故m=0,由二次函数的性质写出单调增区间.
解答 解:若m=1,则函数f(x)=2x+3,则f(-x)=-2x+3≠f(x),此时函数不是偶函数,所以m≠1
若m≠1,且函数f(x)=(m-1)x2+2mx+3是偶函数,
则 一次项2mx=0恒成立,则 m=0,
因此,函数为 f(x)=-x2+3,
∴f(x)的单调递增区间为(-∞,0).
故答案为:(-∞,0).
点评 本题考查函数的奇偶性的应用,以及二次函数的性质,属于基础题.

练习册系列答案
相关题目
15.已知抛物线y=$\frac{{x}^{2}}{4}$与直线y=$\frac{3}{4}$x+1交于点P,Q,则如图所示阴影部分的面积为( )
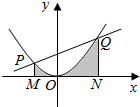

| A. | $\frac{65}{12}$ | B. | $\frac{85}{16}$ | C. | $\frac{143}{24}$ | D. | $\frac{95}{6}$ |