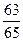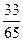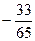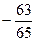题目内容
(本题满分13分)
设两个向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为
钝角,求实数t的取值范围.
设两个向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为
钝角,求实数t的取值范围.
t的取值范围是(-7,-)∪(-,-).
解:由已知,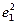 =|e1|2=4,
=|e1|2=4,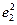 =|e2|2=1,e1·e2=2×1×cos60°=1.
=|e2|2=1,e1·e2=2×1×cos60°=1.
∴(2te1+7e2)·(e1+te2)=2t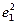 +(2t2+7)e1·e2+7t
+(2t2+7)e1·e2+7t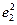 =2t2+15t+7.由2t2+15t+7<0,得-7<t<-.
=2t2+15t+7.由2t2+15t+7<0,得-7<t<-.
由2te1+7e2=λ(e1+te2)(λ<0),得,∴.由于2te1+7e2与e1+te2的夹角为钝角,
故(2te1+7e2)·(e1+te2)<0且2te1+7e2≠λ(e1+te2)(λ<0),
故t的取值范围是(-7,-)∪(-,-).
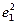 =|e1|2=4,
=|e1|2=4,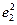 =|e2|2=1,e1·e2=2×1×cos60°=1.
=|e2|2=1,e1·e2=2×1×cos60°=1.∴(2te1+7e2)·(e1+te2)=2t
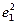 +(2t2+7)e1·e2+7t
+(2t2+7)e1·e2+7t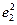 =2t2+15t+7.由2t2+15t+7<0,得-7<t<-.
=2t2+15t+7.由2t2+15t+7<0,得-7<t<-.由2te1+7e2=λ(e1+te2)(λ<0),得,∴.由于2te1+7e2与e1+te2的夹角为钝角,
故(2te1+7e2)·(e1+te2)<0且2te1+7e2≠λ(e1+te2)(λ<0),
故t的取值范围是(-7,-)∪(-,-).

练习册系列答案
相关题目
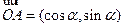 (
(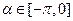 ).向量
).向量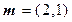 ,
,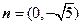 ,
,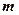
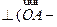
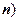 .
.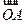 ;
;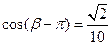 ,
,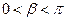 ,求
,求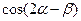 .
.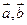 满足
满足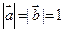 ,且
,且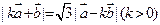 ,令
,令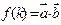 ,
,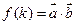 (用
(用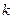 表示);
表示);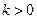 时,
时,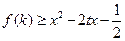 对任意的
对任意的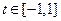 恒成立,求实数
恒成立,求实数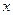 的取值范围。
的取值范围。
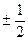
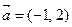 与
与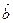 的夹角是
的夹角是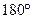 ,且
,且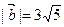 ,则
,则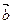 的坐标为( )
的坐标为( )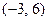
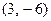
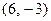
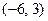
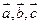 满足
满足 ,且
,且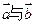 的夹角为135°,
的夹角为135°,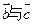 的夹角为120°,
的夹角为120°,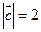 ,则
,则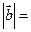 _____________;
_____________; 的最小值是
的最小值是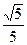 B
B 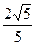 C
C 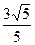 D
D 
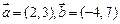 ,则向量
,则向量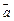 在
在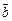 方向上的投影为( )
方向上的投影为( )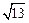
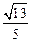
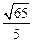
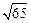
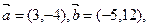 则
则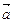 与
与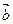 的夹角的
的夹角的 余弦值为( )
余弦值为( )