题目内容
设x>0,y>0,z>0,(Ⅰ)比较
 与
与 的大小;
的大小;(Ⅱ)利用(Ⅰ)的结论,证明:
 .
.
【答案】分析:(Ⅰ)对两个解析式作差,对差的形式进行化简整理,判断出差的符号,得出两数的大小.
(Ⅱ)利用(Ⅰ)类比出一个结论,利用综合法证明不等式即可.
解答:(Ⅰ)∵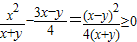 ,∴
,∴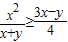 .(5分)
.(5分)
(Ⅱ)由(1)得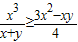 .
.
类似的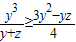 ,
,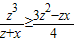 ,(7分)
,(7分)
又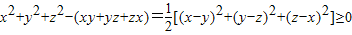 ;
;
∴x2+y2+z2≥xy+yz+zx(9分)(另证:x2+y2≥2xy,y2+z2≥2yz,z2+x2≥2zx,三式相加).
∴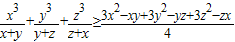 =
=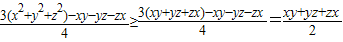 (12分)
(12分)
点评:本题考查综合法与分析法,解题的关键是根据(I)类比出一个条件作为证明的前提.再利用综合法证明,正确理解综合法与分析法的原理与作用,顺利解题很关键.
(Ⅱ)利用(Ⅰ)类比出一个结论,利用综合法证明不等式即可.
解答:(Ⅰ)∵
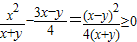 ,∴
,∴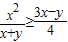 .(5分)
.(5分)(Ⅱ)由(1)得
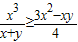 .
.类似的
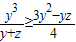 ,
,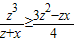 ,(7分)
,(7分)又
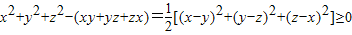 ;
;∴x2+y2+z2≥xy+yz+zx(9分)(另证:x2+y2≥2xy,y2+z2≥2yz,z2+x2≥2zx,三式相加).
∴
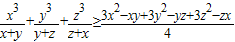 =
=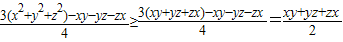 (12分)
(12分)点评:本题考查综合法与分析法,解题的关键是根据(I)类比出一个条件作为证明的前提.再利用综合法证明,正确理解综合法与分析法的原理与作用,顺利解题很关键.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目