题目内容
在锐角△ABC中,2sinAcosB=| 3 |
| 3 |
求:(1)求角C的值;
(2)三角形面积S及边c的长.
分析:(1)利用两角和正弦公式求得 sinC=
,在锐角△ABC中,故有 C=60°.
(2)由韦达定理可得 a+b=2
,ab=2,由余弦定理:c2=a2+b2-2abcosC=(a+b)2-3ab,求得c的值.
| ||
| 2 |
(2)由韦达定理可得 a+b=2
| 3 |
解答:解:(1)由已知2(sinAcosB+cosAsinB)=
.∴2sin(A+B)=
.
又A+B+C=π,∴sinC=
.在锐角△ABC中,C=60°.
(2)由韦达定理,a+b=2
,ab=2,∴S△=
absinC=
,
由余弦定理:c2=a2+b2-2abcosC=(a+b)2-3ab=12-6=6,∴c=
.
| 3 |
| 3 |
又A+B+C=π,∴sinC=
| ||
| 2 |
(2)由韦达定理,a+b=2
| 3 |
| 1 |
| 2 |
| ||
| 2 |
由余弦定理:c2=a2+b2-2abcosC=(a+b)2-3ab=12-6=6,∴c=
| 6 |
点评:本题考查两角和正弦公式,余弦定理的应用,一元二次方程根与系数的关系,求出角C是解题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
 的取值范围是 ________
的取值范围是 ________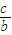 的取值范围是
的取值范围是