题目内容
在锐角△ABC中∠C=2∠B,∠B、∠C的对边长分别是b、c,则| c | b |
分析:根据正弦定理可得到
=
,结合∠C=2∠B根据二倍角公式可得
=
,整理得到
=2cosB,再求得B的范围即可得到
的取值范围.
| c |
| sinC |
| b |
| sinB |
| c |
| 2sinBcosB |
| b |
| sinB |
| c |
| b |
| c |
| b |
解答:解:由正弦定理
=
∵C=2B∴
=
∴
=2cosB
当C为最大角时C<90°∴B<45°
当A为最大角时A<90°∴B>30°
∴30°<B<45°
2cos45°<2cosB<2cos30°
∴
∈(
,
)
故答案为:(
,
).
| c |
| sinC |
| b |
| sinB |
∵C=2B∴
| c |
| 2sinBcosB |
| b |
| sinB |
∴
| c |
| b |
当C为最大角时C<90°∴B<45°
当A为最大角时A<90°∴B>30°
∴30°<B<45°
2cos45°<2cosB<2cos30°
∴
| c |
| b |
| 2 |
| 3 |
故答案为:(
| 2 |
| 3 |
点评:本题主要考查正弦定理和二倍角公式的应用.正弦定理和余弦定理在解三角形中应用比较多,这两个定理和其推论一定要熟练掌握并能够灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的取值范围是 ________
的取值范围是 ________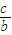 的取值范围是
的取值范围是