题目内容
椭圆C: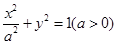 的左右焦点分别为F1,F2,P为椭圆上异于端点的任意的点,PF1,PF2的中点分别为M,N,O为坐标原点,四边形OMPN的周长为2
的左右焦点分别为F1,F2,P为椭圆上异于端点的任意的点,PF1,PF2的中点分别为M,N,O为坐标原点,四边形OMPN的周长为2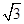 ,则△
,则△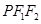 的周长是( )
的周长是( )
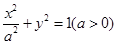 的左右焦点分别为F1,F2,P为椭圆上异于端点的任意的点,PF1,PF2的中点分别为M,N,O为坐标原点,四边形OMPN的周长为2
的左右焦点分别为F1,F2,P为椭圆上异于端点的任意的点,PF1,PF2的中点分别为M,N,O为坐标原点,四边形OMPN的周长为2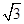 ,则△
,则△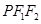 的周长是( )
的周长是( )A. | B. | C. | D. |
A
试题分析:根据椭圆的定义和三角形中位线定理可得 OM+ON+PM+PN= PF1+PF2=2a,即2a=2
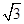 ,解得a=
,解得a=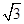 ,由
,由 ,所以c=
,所以c= ,△
,△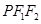 的周长= PF1+PF2+2c=
的周长= PF1+PF2+2c= ,故选A.
,故选A. 
练习册系列答案
相关题目
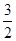 )在椭圆C上.
)在椭圆C上.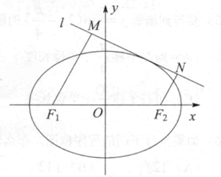
 :
: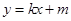 与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且
与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且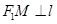 ,
,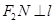 ,四边形
,四边形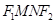 面积S的求最大值.
面积S的求最大值. <4,则曲线
<4,则曲线 和
和 有( )
有( ) 恒有公共点,则实数m的取值范围是( )
恒有公共点,则实数m的取值范围是( )



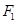 ,
,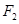 是椭圆的两个焦点,若椭圆上存在点P,使得
是椭圆的两个焦点,若椭圆上存在点P,使得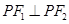 ,则椭圆的离心率的取值范围是( )
,则椭圆的离心率的取值范围是( )



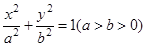 的离心率为
的离心率为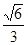 ,且过点
,且过点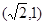 .
.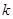 的直线
的直线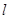 与椭圆相交于不同的两点
与椭圆相交于不同的两点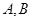 ,试问在
,试问在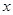 轴上是否存在点
轴上是否存在点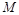 ,使
,使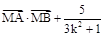 是与
是与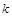 无关的常数?若存在,求出点
无关的常数?若存在,求出点 得顶点
得顶点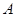 、
、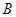 分别是离心率为
分别是离心率为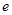 的圆锥曲线
的圆锥曲线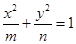 的焦点,顶点
的焦点,顶点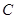 在该曲线上,一同学已正确地推得,当
在该曲线上,一同学已正确地推得,当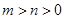 时有
时有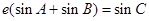 ,类似地,当
,类似地,当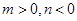 时,有 .
时,有 .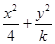 =1的离心率,且e∈(
=1的离心率,且e∈(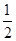 ,1),则实数k的取值范围是 ( )
,1),则实数k的取值范围是 ( ) )
)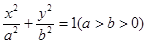 的左、右顶点分别为
的左、右顶点分别为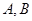 ,左、右焦点分别为
,左、右焦点分别为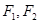 ,若
,若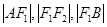 成等比数列,则此椭圆的离心率为( )
成等比数列,则此椭圆的离心率为( )


