题目内容
11.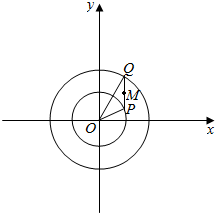 C1,C2是以原点为圆心的两个同心圆,C1的半径r1=2,C2的半径r2=6,C1上有一点P,C2上有一点Q,各以每秒1弧度的角速度绕原点旋转,P点按逆时针方向运动,Q点安顺时针方向运动,当t=0时,P点在x轴上,Q点在y轴上,求PQ中点M的运动轨迹的参数方程.
C1,C2是以原点为圆心的两个同心圆,C1的半径r1=2,C2的半径r2=6,C1上有一点P,C2上有一点Q,各以每秒1弧度的角速度绕原点旋转,P点按逆时针方向运动,Q点安顺时针方向运动,当t=0时,P点在x轴上,Q点在y轴上,求PQ中点M的运动轨迹的参数方程.
分析 设∠POx=θ,则∠QOx=$\frac{π}{2}-θ$,从而P(2cosθ,2sinθ),Q(6sinθ,6cosθ),M(cosθ+3sinθ,sinθ+3cosθ),由辅助角公式,结合θ=ωt=t,能求出PQ中点M的运动轨迹的参数方程.
解答 解:两个点在相同速度相同时间内走过的角度为ωt,
且OP与x轴正半轴的夹角与OQ与x轴正半轴的角之和为$\frac{π}{2}$,
设∠POx=θ,则∠QOx=$\frac{π}{2}-θ$,
∴P(2cosθ,2sinθ),Q(6sinθ,6cosθ),
则PQ的中点为M,由中点坐标公式得$\left\{\begin{array}{l}{{x}_{M}=cosθ+3sinθ}\\{{y}_{M}=sinθ+3cosθ}\end{array}\right.$,
∴M(cosθ+3sinθ,sinθ+3cosθ),
由辅助角公式,得:
${x}_{M}=cosθ+3sinθ=\sqrt{10}cos(θ-α)$,$(cosα=\frac{\sqrt{10}}{10})$.
${y}_{M}=sinθ+3cosθ=\sqrt{10}sin(θ+α)$,
又θ=ωt=t,
∴PQ中点M的运动轨迹的参数方程为$\left\{\begin{array}{l}{x=\sqrt{10}cos(t-α)}\\{y=\sqrt{10}sin(t-α)}\end{array}\right.$.(t为参数),$(cosα=\frac{\sqrt{10}}{10})$.
点评 本题考查线段中点的运动轨迹方程的求法,是中档题,解题时要认真审题,注意中点坐标公式、和差化积公式的合理运用.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
1.函数f(x)=loga(4-ax)在区间[0,2]上是减函数,则实数a的取值范围是( )
| A. | (0,1) | B. | (1,2) | C. | (0,2) | D. | (2,+∞) |
2.已知圆O:x2+y2=16,在圆O上随机取两点A、B,使|AB|≤4$\sqrt{3}$的概率为( )
| A. | $\frac{9}{15}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
6.已知sinα+cosα=-$\frac{1}{2}$,α∈(0,π),则tanα=( )
| A. | $\frac{-4+\sqrt{7}}{3}$ | B. | $\frac{-4±\sqrt{7}}{3}$ | C. | $\frac{4-\sqrt{7}}{3}$ | D. | $\frac{-4-\sqrt{7}}{3}$ |