题目内容
3.设函数f(x)=sin(ωx+φ),其中ω>0,|φ|<$\frac{π}{2}$,若cos$\frac{π}{3}cosφ-sin\frac{2π}{3}$sinφ=0,且图象的两条对称轴间的最近距离是$\frac{π}{2}$.(1)求函数f(x)的解析式;
(2)若A,B,C是△ABC的三个内角,且f(A)=-1,求sinB+sinC的取值范围.
分析 (1)利用两角差的余弦函数公式及余弦函数的图象和性质可求φ=$\frac{π}{6}$+kπ,k∈Z,结合范围|φ|<$\frac{π}{2}$,可求φ,
由题意可求周期为T=π,利用周期公式可求ω,从而可得函数解析式.
(2)由题意可得sin(2x+$\frac{π}{6}$)=-1,结合范围0<A<π,可解得A=$\frac{2π}{3}$,从而B+C=$\frac{π}{3}$,利用三角函数恒等变换的应用可将sinB+sinC化为sin(B+$\frac{π}{3}$),结合范围0<B<$\frac{π}{3}$,利用正弦函数的图象和性质即可求其取值范围.
解答 (本题满分为14分)
解:(1)∵cos$\frac{π}{3}cosφ-sin\frac{2π}{3}$sinφ=cos($\frac{π}{3}$+φ)=0,
∴$\frac{π}{3}$+φ=$\frac{π}{2}$+kπ,得φ=$\frac{π}{6}$+kπ,k∈Z
∵|φ|<$\frac{π}{2}$,∴取k=0,得φ=$\frac{π}{6}$,
∵函数f(x)图象的一条对称轴离一个对称中心的最近距离是$\frac{π}{4}$,
∴周期为T=π,得ω=$\frac{2π}{T}$=2,得f(x)=sin(2x+$\frac{π}{6}$).…(6分)
(2)由f(A)=-1,得sin(2x+$\frac{π}{6}$)=-1,
∵A是△ABC的内角,0<A<π,
∴$\frac{π}{6}$<2A+$\frac{π}{6}$<$\frac{13π}{6}$,得2A+$\frac{π}{6}$=$\frac{3π}{2}$,
∴A=$\frac{2π}{3}$,从而B+C=$\frac{π}{3}$.
由sinB+sinC=sinB+sin($\frac{π}{3}$-B)=$\frac{\sqrt{3}}{2}$cosB+$\frac{1}{2}$sinB
∴sinB+sinC=sin(B+$\frac{π}{3}$),…(12分)
∵0<B<$\frac{π}{3}$,$\frac{π}{3}$<B+$\frac{π}{3}$<$\frac{2π}{3}$,
∴$\frac{\sqrt{3}}{2}$<sin(B+$\frac{π}{3}$)≤1,即sinB+sinC∈($\frac{\sqrt{3}}{2}$,1].
因此,sinB+sinC的取值范围是($\frac{\sqrt{3}}{2}$,1].…(14分)
点评 本题主要考查了两角差的余弦函数公式,正弦函数、余弦函数的图象和性质,周期公式,三角函数恒等变换的应用,考查了计算能力和转化思想,属于中档题.

 全优点练单元计划系列答案
全优点练单元计划系列答案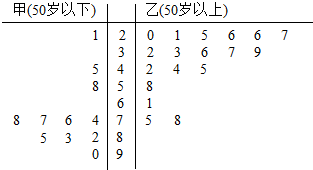 某学生对其亲属30人的饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉食为主)
某学生对其亲属30人的饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉食为主)(1)根据以上数据完成下列2×2列联表:
| 主食蔬菜 | 主食肉类 | 合计 | |
| 50岁以下 | |||
| 50岁以上 | |||
| 合计 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| A. | $\frac{a}{2}$ | B. | $\frac{2}{a}$ | C. | 1+a | D. | 1-a |
| A. | -$\frac{1}{4}$ | B. | $\frac{5}{8}$ | C. | -$\frac{7}{16}$ | D. | $\frac{9}{16}$ |
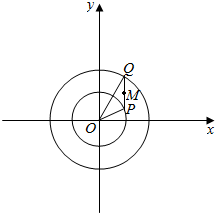 C1,C2是以原点为圆心的两个同心圆,C1的半径r1=2,C2的半径r2=6,C1上有一点P,C2上有一点Q,各以每秒1弧度的角速度绕原点旋转,P点按逆时针方向运动,Q点安顺时针方向运动,当t=0时,P点在x轴上,Q点在y轴上,求PQ中点M的运动轨迹的参数方程.
C1,C2是以原点为圆心的两个同心圆,C1的半径r1=2,C2的半径r2=6,C1上有一点P,C2上有一点Q,各以每秒1弧度的角速度绕原点旋转,P点按逆时针方向运动,Q点安顺时针方向运动,当t=0时,P点在x轴上,Q点在y轴上,求PQ中点M的运动轨迹的参数方程.