题目内容
1.函数f(x)=loga(4-ax)在区间[0,2]上是减函数,则实数a的取值范围是( )| A. | (0,1) | B. | (1,2) | C. | (0,2) | D. | (2,+∞) |
分析 先将函数f(x)=loga(4-ax)转化为y=logat,t=4-ax两个基本函数,再利用复合函数的单调性求解.
解答 解:令y=logat,t=4-ax,
①若0<a<1,则函y=logat,是减函数,
由题设知t=4-ax为增函数,需a<0,故此时无解.
(2)若a>1,则函数y=logat是增函数,则t为减函数,
需a>0,且4-a×2>0,可解得1<a<2,
综上可得实数a 的取值范围是(1,2).
故选:B.
点评 本题考查复合函数的单调性,关键是分解为两个基本函数,利用同增异减的结论研究其单调性,再求参数的范围,属于中档题.

练习册系列答案
相关题目
12.已知圆(x-1)2+(y+1)2=4关于直线mx+y-2m=0对称,则m的值为( )
| A. | 1 | B. | -1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
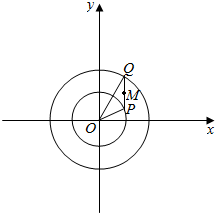 C1,C2是以原点为圆心的两个同心圆,C1的半径r1=2,C2的半径r2=6,C1上有一点P,C2上有一点Q,各以每秒1弧度的角速度绕原点旋转,P点按逆时针方向运动,Q点安顺时针方向运动,当t=0时,P点在x轴上,Q点在y轴上,求PQ中点M的运动轨迹的参数方程.
C1,C2是以原点为圆心的两个同心圆,C1的半径r1=2,C2的半径r2=6,C1上有一点P,C2上有一点Q,各以每秒1弧度的角速度绕原点旋转,P点按逆时针方向运动,Q点安顺时针方向运动,当t=0时,P点在x轴上,Q点在y轴上,求PQ中点M的运动轨迹的参数方程.