题目内容
【题目】已知椭圆![]() 的左右焦点为
的左右焦点为![]() ,
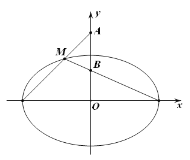
,![]() 是椭圆上半部分的动点,连接
是椭圆上半部分的动点,连接![]() 和长轴的左右两个端点所得两直线交
和长轴的左右两个端点所得两直线交![]() 正半轴于
正半轴于![]() 两点(点
两点(点![]() 在
在![]() 的上方或重合).
的上方或重合).
(1)当![]() 面积
面积![]() 最大时,求椭圆的方程;
最大时,求椭圆的方程;
(2)当![]() 时,在
时,在![]() 轴上是否存在点
轴上是否存在点![]() 使得
使得![]() 为定值,若存在,求
为定值,若存在,求![]() 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
【答案】(1) (2)存在,
(2)存在,![]()
【解析】
(1)由椭圆的方程,可得![]() ,结合三角形的面积公式和基本不等式,求得
,结合三角形的面积公式和基本不等式,求得![]() ,进而求得椭圆的方程;
,进而求得椭圆的方程;
(2)设![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,分别求得
,分别求得![]() 的坐标,根据向量的数量积的运算,即可求解.
的坐标,根据向量的数量积的运算,即可求解.
(1)由题意,椭圆![]() ,可得
,可得![]() ,
,
则![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
又由![]() ,解得
,解得![]() ,
,
所以椭圆方程为: ;
;
(2)由题意,当![]() 时,椭圆的
时,椭圆的![]() ,
,
假设存在点![]() ,使得
,使得![]() 为定值,设
为定值,设![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
由 ,消去
,消去![]() 可得
可得![]() ,可得
,可得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() 的定值,
的定值,
所以![]() ,即
,即![]() ,故点
,故点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目


