题目内容
【题目】已知平面直角坐标系内的动点P到直线![]() 的距离与到点
的距离与到点![]() 的距离比为
的距离比为![]() .
.
(1)求动点P所在曲线E的方程;
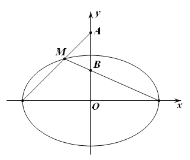
(2)设点Q为曲线E与![]() 轴正半轴的交点,过坐标原点O作直线
轴正半轴的交点,过坐标原点O作直线![]() ,与曲线E相交于异于点
,与曲线E相交于异于点![]() 的不同两点
的不同两点![]() ,点C满足
,点C满足![]() ,直线
,直线![]() 和
和![]() 分别与以C为圆心,
分别与以C为圆心,![]() 为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比
为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1) 设动点P的坐标为![]() , 由题意可得
, 由题意可得![]() ,整理可得曲线E的方程;
,整理可得曲线E的方程;
(2) 解法一:可得圆C方程为![]() ,设直线MQ的方程为
,设直线MQ的方程为![]() ,设直线NQ的方程为
,设直线NQ的方程为![]() ,分别与圆联立,可得
,分别与圆联立,可得![]() ,
,![]() ,可得
,可得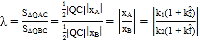 ,可得
,可得![]() ,代入可得答案;
,代入可得答案;
解法二:可得圆C方程为![]() ,设直线MQ的方程为
,设直线MQ的方程为![]() ,则点C到MQ的距离为
,则点C到MQ的距离为![]() ,
,![]()
![]() ,
,![]()
![]() ,设直线NQ的方程为
,设直线NQ的方程为![]() ,同理可得:
,同理可得:![]()
![]() ,
,![]() ,可得
,可得![]() ,代入可得答案.
,代入可得答案.
解:(1)设动点P的坐标为![]() ,由题意可得
,由题意可得![]() ,
,
整理,得:![]() ,即
,即![]() 为所求曲线E的方程;
为所求曲线E的方程;
(2)(解法一)由已知得:![]() ,
,![]() ,
,![]() ,即圆C方程为
,即圆C方程为![]()
由题意可得直线MQ,NQ的斜率存在且不为0
设直线MQ的方程为![]() ,与
,与![]() 联立得:
联立得:![]()
所以,![]()
同理,设直线NQ的方程为![]() ,与
,与![]() 联立得:
联立得:![]()
所以![]()
因此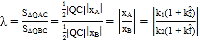
由于直线![]() 过坐标原点,所以点
过坐标原点,所以点![]() 与点
与点![]() 关于坐标原点对称
关于坐标原点对称
设![]() ,
,![]() ,所以,
,所以,![]()
又![]() 在曲线
在曲线![]() 上,所以
上,所以![]() ,即
,即![]()
故![]() ,
,
由于![]() ,所以,
,所以,![]()
(解法二)由已知得:![]() ,
,![]() ,
,![]() ,即圆C方程为
,即圆C方程为![]()
由题意可得直线MQ,NQ的斜率存在且不为0
设直线MQ的方程为![]() ,则点C到MQ的距离为
,则点C到MQ的距离为![]()
所以![]()
于是,![]()
![]()
设直线NQ的方程为![]() ,同理可得:
,同理可得:![]()
![]()
所以![]()
由于直线l过坐标原点,所以点M与点N关于坐标原点对称
设![]() ,
,![]() ,所以,
,所以,![]()
又![]() 在曲线
在曲线![]() 上,所以
上,所以![]() ,即
,即![]()
故![]() ,
,
由于![]() ,所以,
,所以,![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目