题目内容
【题目】为践行“绿水青山就是金山银山”的发展理念,贵阳一中“保护饮用水源地”课题研究小组的同学们对红枫湖、百花湖、阿哈水库、花溪水库、北郊水库5处水源地进行了样本采集并送环保部门进行水质检测.已知5处水源地中有1处被某污染物污染,需要通过检测水源样本来确定被污染的水源地现有三个检測方案:
方案甲:对5个样本逐个检测,直到能确定被污染的水源地为止.
方案乙:先任取1个样本进行检测,若检测到污染物,则检测结束;若未检测到污染物,则在剩余4个样本中任取2个,并将这2个样本取部分混合在一起检测,若检测到污染物,则再在这2个样本中任取一个检测,否则在剩余2个未检测样本中任取一个检测.
方案丙:先任取2个样本,并将这2个样本取部分混合在一起检测,若检测到污染物,则再在这2个样本中任取一个检测;若未检测到污染物,则对剩余3个未检测样本进行逐个检测,直到能确定被污染的水源地为止.假设随机变量![]() 分别表示用方案甲、方案乙、方案丙进行检测所需的检测次数.
分别表示用方案甲、方案乙、方案丙进行检测所需的检测次数.
(1)求![]() 能取到的最大值和其对应的概率;
能取到的最大值和其对应的概率;
(2)求![]() 的期望假设每次检测的费用都相同,请从经济角度说明方案乙和方案丙哪一个更适合?
的期望假设每次检测的费用都相同,请从经济角度说明方案乙和方案丙哪一个更适合?
【答案】(1)![]() 的最大值为4,
的最大值为4,![]() ;
;![]() 的最大值为3,
的最大值为3,![]() ;
;![]() 的最大值为3,
的最大值为3,![]() (2)方案丙更适合
(2)方案丙更适合
【解析】
(1)根据题意可分析得到用方案甲最多需检测4次,即前3次均未检测到污染物;用方案乙最多需检测3次,即先任取1个样本进行检测时未检测到污染物;用方案丙最多需检测3次,即先任取2个样本混合检测时未检测到污染物,且对剩余3个样本检测时第一次未检测到污染物,分别求得概率即可;
(2)![]() 的可能取值为1,3,由(1)可得
的可能取值为1,3,由(1)可得![]() ,即可求得
,即可求得![]() ;
;![]() 的可能取值为2,3,由(1)可得
的可能取值为2,3,由(1)可得![]() ,即可求得
,即可求得![]() ,比较
,比较![]() 与
与![]() ,越小的越合适.
,越小的越合适.
解:(1)用方案甲最多需检测4次,即前3次均未检测到污染物,
则![]() 的最大值为4,所以
的最大值为4,所以![]() ;
;
用方案乙最多需检测3次,即先任取1个样本进行检测时未检测到污染物,
则![]() 的最大值为3,
的最大值为3,![]() ;
;
用方案丙最多需检测3次,即先任取2个样本混合检测时未检测到污染物,且对剩余3个样本检测时第一次未检测到污染物,
则![]() 的最大值为3,
的最大值为3,![]() .
.
(2)![]() 的可能取值为1,3,由(1)可知
的可能取值为1,3,由(1)可知![]() ,所以
,所以![]() ,
,
则![]() ;
;
![]() 的可能取值为2,3,由(1)可知
的可能取值为2,3,由(1)可知![]() ,所以
,所以![]() ,
,
![]() ,
,
因为![]() ,所以方案丙所需的检测次数期望较少,所需的检测费用期望较低,所以方案丙更适合.
,所以方案丙所需的检测次数期望较少,所需的检测费用期望较低,所以方案丙更适合.

【题目】某家电公司进行关于消费档次的调查,根据家庭年均家电消费额将消费档次分为4组:不超过3000元、超过3000元且不超过5000元、超过5000元且不超过10000元、超过10000元,从A、B两市中各随机抽取100个家庭,统计数据如下表所示:
消费 档次 | 不超过3000元 | 超过3000元 且不超过5000元 | 超过5000元 且不超过10000元 | 超过10000元 |
A市 | 20 | 50 | 20 | 10 |
B市 | 50 | 30 | 10 | 10 |
年均家电消费额不超过5000元的家庭视为中低消费家庭,超过5000元的视为中高消费家庭.
(1)从A市的100个样本中任选一个家庭,求此家庭属于中低消费家庭的概率;
(2)现从A、B两市中各任选一个家庭,分别记为甲、乙,估计甲的消费档次不低于乙的消费档次的概率;
(3)以各消费档次的区间中点对应的数值为该档次的家庭年均家电消费额,估计A、B两市中,哪个市的家庭年均家电消费额的方差较大(直接写出结果,不必说明理由).
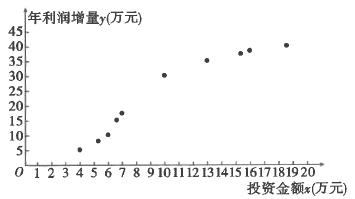
【题目】某果园种植“糖心苹果”已有十余年,为了提高利润,该果园每年投入一定的资金,对种植采摘包装宣传等环节进行改进.如图是2009年至2018年,该果园每年的投资金额![]() (单位:万元)与年利润增量
(单位:万元)与年利润增量![]() (单位:万元)的散点图:
(单位:万元)的散点图:
该果园为了预测2019年投资金额为20万元时的年利润增量,建立了![]() 关于
关于![]() 的两个回归模型;
的两个回归模型;
模型①:由最小二乘公式可求得![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() ;
;
模型②:由图中样本点的分布,可以认为样本点集中在曲线:![]() 的附近,对投资金额
的附近,对投资金额![]() 做交换,令
做交换,令![]() ,则
,则![]() ,且有
,且有![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)分别利用这两个回归模型,预测投资金额为20万元时的年利润增量(结果保留两位小数);
(3)根据下列表格中的数据,比较两种模型的相关指数![]() ,并说明谁的预测值精度更高更可靠.
,并说明谁的预测值精度更高更可靠.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 102.28 | 36.19 |
附:样本![]() 的最小乘估计公式为
的最小乘估计公式为 ,
,![]() ;
;
相关指数 .
.
参考数据:![]() ,
,![]() .
.