题目内容
【题目】已知不等式|2x-1|+|2x-2|＜x+3的解集是A．
（Ⅰ）求集合A；
（Ⅱ）设x，y∈A，对任意a∈R，求证：xy（||x+a|-|y+a||）＜x2+y2．
【答案】（Ⅰ）A={x|0＜x＜2}（Ⅱ）见解析
【解析】
（Ⅰ）利用零点分类法，进行求解不等式；
（Ⅱ）利用绝对值不等式的性质和基本不等式进行证明。
解：（Ⅰ）当x＜
时，不等式变形为1-2x+2-2x＜x+3，解得0＜x＜；
当
时，不等式变形为2x-1+2-2x＜x+3，解得；
当x＞1时，不等式变形为2x-1+2x-2＜x+3，解得1＜x＜2；
综上得A={x|0＜x＜2}．
（Ⅱ）∵x，y∈A，∴0＜x，y＜2，
∵||x+a|-|y+a||≤|（x+a）-（y+a）|=|x-y|，
∵0＜x，y＜2，∴-2＜x-y＜2，∴|x-y|＜2，∴||x+a|-|y+a||＜2，
∵
+
≥2
=2，∴||x+a|-|y+a||＜+，即xy（|x+a|-|y+a|）＜x2+y2．
练习册系列答案
相关题目
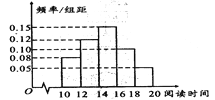
【题目】某教师将寒假期间该校所有学生阅读小说的时间统计如下图所示，并统计了部分学生阅读小说的类型，得到的数据如下表所示：
男生 | 女生 | |
阅读武侠小说 | 80 | 30 |
阅读都市小说 | 20 | 70 |
（1）是否有99.9%的把握认为“性别”与“阅读小说的类型”有关？
（2）求学生阅读小说时间的众数和平均数（同一组数据用该组区间的中点值作代表）；
（3）若按照分层抽样的方法从阅读时间在
、
的学生中随机抽取6人，再从这6人中随机挑选2人介绍选取小说类型的缘由，求所挑选的2人阅读时间都在的概率.
附：
，
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
