题目内容
已知等差数列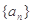 中,公差
中,公差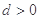 ,其前
,其前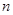 项和为
项和为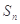 ,且满足:
,且满足: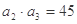 ,
,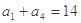 .
.
(Ⅰ)求数列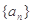 的通项公式;
的通项公式;
(Ⅱ)令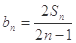 ,
, 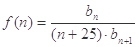 (
(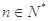 ),求
),求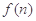 的最大值.
的最大值.
【答案】
(1)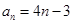 ;(2)
;(2) 取得最大值
取得最大值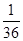 .
.
【解析】
试题分析:本题主要考查等差数列的通项公式、前n项和公式、等差数列的性质和基本不等式等基础知识,考查思维能力、分析问题解决问题的能力、运算能力等.第一问,先利用等差数列的性质将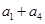 转化成
转化成 ,再结合
,再结合 的值,联立解出
的值,联立解出 和
和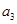 ,求出
,求出 和
和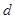 ,写出通项公式;第二问,先利用等差数列的前n项和公式求
,写出通项公式;第二问,先利用等差数列的前n项和公式求 ,代入到
,代入到 中,再将结果代入到
中,再将结果代入到 中,上下同除以
中,上下同除以 ,利用基本不等式求最值,要注意等号成立的条件.
,利用基本不等式求最值,要注意等号成立的条件.
试题解析:∵数列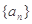 是等差数列,
是等差数列,
∴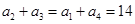 ,又
,又 ,
,
∴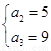 或
或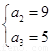 ,
,
∵公差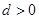 ,∴
,∴ 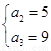 ,
,
∴ ,
, ,
,
∴ .
.
(2)∵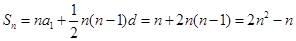 ,
,
∴ ,
,
∴ .
.
当且仅当 ,即
,即 时,
时, 取得最大值
取得最大值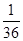 .
.
考点:1.等差数列的通项公式;2.等差数列的性质;3.等差数列的前n项和;4.基本不等式.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
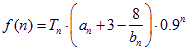 (
(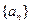 中,公差
中,公差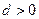 ,其前
,其前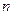 项和为
项和为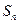 ,且满足
,且满足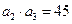 ,
,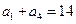 .
.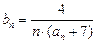 (
(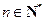 ),数列
),数列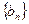 的前
的前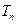 ,求证:
,求证: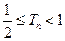 ;
;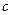 (
(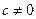 ),
),  使得数列
使得数列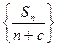 为等差数列?若存在,试求出
为等差数列?若存在,试求出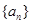 中,公差
中,公差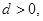 又
又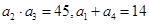 .
.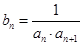 ,数列
,数列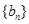 的前
的前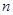 项和记为
项和记为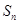 ,求
,求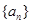 中,公差
中,公差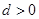 ,其前
,其前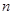 项和为
项和为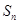 ,且满足
,且满足 ,
,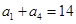 .
.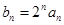 (
( ),求数列
),求数列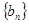 的前
的前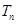 ;
;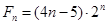 ,试比较
,试比较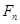 与
与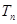 的大小.
的大小.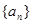 中,公差
中,公差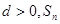 为其前n项和,且满足:
为其前n项和,且满足: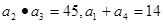 。
。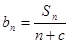 构造一个新的数列
构造一个新的数列 ,使
,使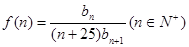 的最大值。
的最大值。