题目内容
二次函数f(x)的二次项系数为正数,且对任意xÎR都有f(x)=f(4-x)成立,
若f(2-a2)<f(1+a-a2),那么a的取值范围是 ( )
| A.1<a<2 | B.a>1 | C.a>2 | D.a<1 |
D
解析试题分析:因为,二次函数f(x)的二次项系数为正数,且对任意xÎR都有f(x)=f(4-x)成立,所以二次函数图象开口向上,对称轴为x=2,而2-a2 2, 1+a-a2
2, 1+a-a2
=

 <2,故由f(2-a2)<f(1+a-a2)得,2-a2>1+a-a2,解得,a<1,选D。
<2,故由f(2-a2)<f(1+a-a2)得,2-a2>1+a-a2,解得,a<1,选D。
考点:主要考查二次函数的图象和性质,一元二次不等式解法。
点评:中档题,利用二次函数的图象和性质,将抽象不等式转化成具体不等式,利用不等式的解法等基础知识,达到解题目的。

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
设
| A.a<c<b | B.b<c<a | C.a<b<c | D.b<a<c |
已知函数 若存在
若存在 ,则实数
,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
夏季高山上温度从山脚起每升高100米,降低0.7℃,已知山顶的温度是14.1℃,山脚的温度是26℃,则山的相对高度是( ) 米.
| A.1800 | B.1700 | C.1600 | D.1500 |
若点A(-1, ),B(0,
),B(0, ),C(4,
),C(4, )在二次函数
)在二次函数 (
( 为常数)的图像上,则
为常数)的图像上,则 ,
, ,
, 的大小关系为:
的大小关系为:
A. ﹤ ﹤ ﹤ ﹤ | B. ﹤ ﹤ ﹤ ﹤ | C. ﹤ ﹤ ﹤ ﹤ | D. ﹤ ﹤ ﹤ ﹤ |
若 且
且 ,在定义域
,在定义域 上满足
上满足 ,则
,则 的取值范围是( )
的取值范围是( )
| A.(0,1) | B.[ ,1) ,1) | C.(0, ] ] | D.(0,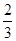 ] ] |
 ,(
,( ,且
,且 ),若数列
),若数列 满足
满足 ,且
,且 的取值范围是( )
的取值范围是( )


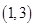
 的x取值范围是 ( )
的x取值范围是 ( )



 ,
, ,且
,且 ,当
,当 时,
时, ,
, ,
, ,则
,则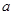 、
、 、
、 的大小顺序是( )。
的大小顺序是( )。 .
. 
 .
. 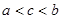
 .
. 
 .
. 