题目内容
已知函数 ,(
,( ,且
,且 ),若数列
),若数列 满足
满足 ,且
,且 是递增数列,则实数
是递增数列,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.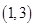 |
C
解析试题分析:因为,函数 ,(
,( ,且
,且 ),且数列
),且数列 满足
满足 ,且
,且 是递增数列,所以,
是递增数列,所以,  =
= 在(1,+∞),
在(1,+∞), 是增函数.由复合函数的单调性,
是增函数.由复合函数的单调性,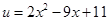 在(
在( ,+∞)是增函数,所以,a>1,且
,+∞)是增函数,所以,a>1,且 ,解得,
,解得,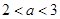 ,故选C。
,故选C。
考点:分段函数的概念,一次函数、指数函数的单调性,数列的性质,复合函数的单调性。
点评:易错题,注意运用转化思想,将数列的递增,转化成研究函数在某区间是增函数。复合函数的单调性,遵循“内外层函数,同增异减”。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数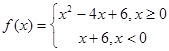 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. | B. |
C.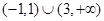 | D. |
下图给出4个幂函数的图像,则图像与函数的大致对应是 
A. | B. |
C. | D. |
已知函数 ,则
,则 的值是 ( )
的值是 ( )
A. | B. | C. | D. |
若函数 ,则
,则 的值是( )
的值是( )
| A.9 | B. | C.-9 | D. |
已知函数 下列命题正确的是 ( )
下列命题正确的是 ( )
A.若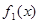 是增函数, 是增函数, 是减函数,则 是减函数,则 存在最大值 存在最大值 |
B.若 存在最大值,则 存在最大值,则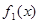 是增函数, 是增函数, 是减函数 是减函数 |
C.若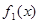 , , 均为减函数,则 均为减函数,则 是减函数 是减函数 |
D.若 是减函数,则 是减函数,则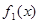 , , 均为减函数 均为减函数 |
已知函数 ,若
,若 ,
, ,
, ,则 ( )
,则 ( )
A. | B. | C. | D. |
设函数 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. | B. |
C. | D. |
二次函数f(x)的二次项系数为正数,且对任意xÎR都有f(x)=f(4-x)成立,
若f(2-a2)<f(1+a-a2),那么a的取值范围是 ( )
| A.1<a<2 | B.a>1 | C.a>2 | D.a<1 |