题目内容
设
| A.a<c<b | B.b<c<a | C.a<b<c | D.b<a<c |
D
解析试题分析:由对数函数的性质,
所以,b<a<c,故选D。
考点:本题主要考查对数函数的性质。
点评:简单题,涉及比较函数值的大小问题,首先考虑函数的单调性,必要时引入“-1,0,1”等作为“媒介”。

练习册系列答案
相关题目
下图给出4个幂函数的图像,则图像与函数的大致对应是 
A. | B. |
C. | D. |
已知函数 ,若
,若 ,
, ,
, ,则 ( )
,则 ( )
A. | B. | C. | D. |
设函数 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. | B. |
C. | D. |
下列大小关系正确的是
A. | B. |
C. | D. |
若方程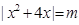 有实数根,则所有实数根的和可能为
有实数根,则所有实数根的和可能为
| A.-2,-4,-6 | B.-4,-5,-6 | C.-3,-4,-5 | D.-4,-6,-8 |
已知 (
( >0,
>0, >0,
>0, ≠1),
≠1), , 则
, 则 的值为( )
的值为( )
A. | B.  | C.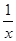 | D. |
二次函数f(x)的二次项系数为正数,且对任意xÎR都有f(x)=f(4-x)成立,
若f(2-a2)<f(1+a-a2),那么a的取值范围是 ( )
| A.1<a<2 | B.a>1 | C.a>2 | D.a<1 |
已知函数y=4x-3×2x+3,当其值域为[1,7]时,则变量x的取值范围是
| A.[2,4] | B.(-∞,0] |
| C.(0,1]∪[2,4] | D.(-∞,0]∪[1,2] |