题目内容
本题满分14分)
已知函数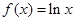 ,
,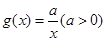 ,设
,设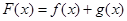 .
.
(Ⅰ)求函数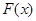 的单调区间;
的单调区间;
(Ⅱ)若以函数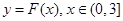 图像上任意一点
图像上任意一点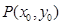 为切点的切线的斜率
为切点的切线的斜率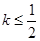 恒成立,求实数
恒成立,求实数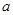 的最小值;
的最小值;
(Ⅲ)是否存在实数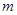 ,使得函数
,使得函数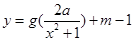 的图像与函数
的图像与函数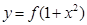 的图像恰有四个不同的交点?若存在,求出实数
的图像恰有四个不同的交点?若存在,求出实数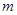 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】
解:(Ⅰ)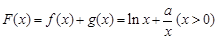 ,
,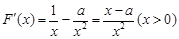 .
.
∵  ,由
,由 ,∴
,∴  在
在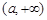 上单调递增;
上单调递增;
由 ,∴
,∴  在
在 上单调递减.
上单调递减.
∴  的单调递减区间为
的单调递减区间为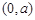 ,单调递增区间为
,单调递增区间为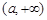 .……………4分
.……………4分
(Ⅱ)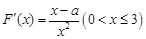 ,
,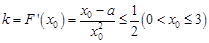 恒成立
恒成立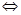

当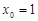 时,
时, 取得最大值
取得最大值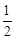 ,∴
,∴ 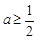 ,∴
,∴ 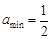 .……………8分
.……………8分
(Ⅲ)若 的图象与
的图象与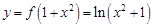 的图象恰有四个不同得交点,即
的图象恰有四个不同得交点,即 有四个不同的根,亦即
有四个不同的根,亦即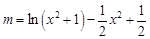 有四个不同的根.
有四个不同的根.
令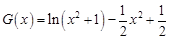 ,则
,则 ,
,
当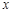 变化时,
变化时,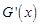 、
、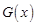 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
+ |
- |
+ |
- |
|
|
|
|
|
|
由表格知: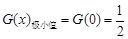 ,
,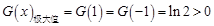 .
.
又∵ 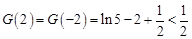 可知,当
可知,当 时,
时,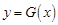 与
与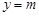

恰有四个不同的交点.
∴当 时,
时,
 的图象
的图象
与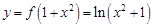 的图象恰有四个不同的交点. ………………14分
的图象恰有四个不同的交点. ………………14分
【解析】略

练习册系列答案
相关题目
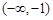
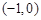
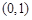


 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
