题目内容
设向量a=(x2-3,1),b=(2x,-y)(其中实数y和x不同时为零),当|x|>1时,有a⊥b;当|x|≤1时,有a∥b.
(Ⅰ)求函数解析式y=f(x);
(Ⅱ)设α∈(0,
),且f(sinα)=
,求α.
(Ⅰ)求函数解析式y=f(x);
(Ⅱ)设α∈(0,
| π |
| 2 |
| 1 |
| 2 |
分析:(Ⅰ)根据题意分类讨论,当|x|>1时由
⊥
,可得函数解析式;|x|≤1时由
∥
,可得其函数表达式;两者合起来即可;
(Ⅱ)由(Ⅰ)可知道,α∈(0,
),由f(sinα)=
即得
=
,从而可求得sinα=
-2,利用反正弦可求得α.
| a |
| b |
| a |
| b |
(Ⅱ)由(Ⅰ)可知道,α∈(0,
| π |
| 2 |
| 1 |
| 2 |
| 2sinα |
| 3-sin2α |
| 1 |
| 2 |
| 7 |
解答:解:(Ⅰ)∵当|x|>1时
⊥
,
∴(x2-3)•2x-y=0,
∴y=2x3-6x(|x|>1)(2分)
∵当|x|≤1时
∥
,
∴(x2-3)•(-y)=2x,
∵实数y和x不同时为零,
∴y=
(|x|≤1,且x≠0)(4分)
∴y=f(x)=
(6分)
(Ⅱ)由|sinα|≤1且f(sinα)=
,
∴有
=
,(8分)
∴sin2α+4sinα-3=0,(sinα+2)2=7,
∴sinα=±
-2(舍负),且有0<
-2<1(10分)
又∵α∈(0,
),
∴α=arcsin(
-2)(12分)
| a |
| b |
∴(x2-3)•2x-y=0,
∴y=2x3-6x(|x|>1)(2分)
∵当|x|≤1时
| a |
| b |
∴(x2-3)•(-y)=2x,
∵实数y和x不同时为零,
∴y=
| 2x |
| 3-x2 |
∴y=f(x)=
|
(Ⅱ)由|sinα|≤1且f(sinα)=
| 1 |
| 2 |
∴有
| 2sinα |
| 3-sin2α |
| 1 |
| 2 |
∴sin2α+4sinα-3=0,(sinα+2)2=7,
∴sinα=±
| 7 |
| 7 |
又∵α∈(0,
| π |
| 2 |
∴α=arcsin(
| 7 |
点评:本题考查三角函数的化简求值,着重考查平面向量的坐标表示及垂直与平行的应用,难点在于反正弦的理解与应用,属于中档题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
 ,且
,且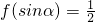 ,求α.
,求α. ,且
,且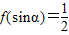 ,求α.
,求α.