题目内容
设函数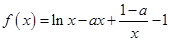 .
.
(1)当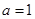 时,求曲线
时,求曲线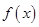 在
在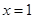 处的切线方程;
处的切线方程;
(2)当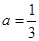 时,求函数
时,求函数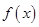 的单调区间;
的单调区间;
(3)在(2)的条件下,设函数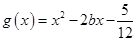 ,若对于
,若对于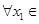 [1,2],
[1,2],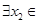 [0,1],使
[0,1],使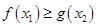 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)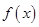 在
在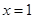 处的切线方程为
处的切线方程为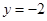 ;(2)函数
;(2)函数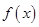 的单调增区间为
的单调增区间为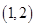 ;单调减区间为
;单调减区间为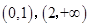 ;(3)
;(3)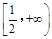 .
.
解析试题分析:(1)首先求函数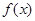 的定义域,利用导数的几何意义求得
的定义域,利用导数的几何意义求得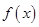 在
在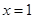 处的切线的斜率,再利用直线的点斜式方程求得
处的切线的斜率,再利用直线的点斜式方程求得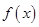 在
在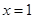 处的切线方程;(2)分别解不等式
处的切线方程;(2)分别解不等式 可得函数的单调递增区间、单调递减区间;(3)由已知“对于
可得函数的单调递增区间、单调递减区间;(3)由已知“对于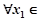 [1,2],
[1,2],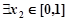 使
使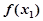 ≥
≥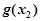 成立”
成立”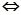
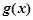 在
在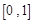 上的最小值不大于
上的最小值不大于 在
在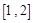 上的最小值,先分别求函数
上的最小值,先分别求函数 ,
,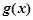 的最小值,最后解不等式
的最小值,最后解不等式 得实数
得实数 的取值范围.
的取值范围.
试题解析:函数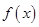 的定义域为
的定义域为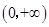 , 1分
, 1分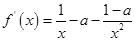 2分
2分
(1)当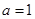 时,
时,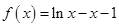 ,
,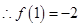 , 3分
, 3分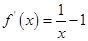 ,
,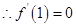 , 4分
, 4分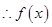 在
在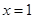 处的切线方程为
处的切线方程为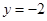 . 5分
. 5分
(2)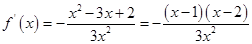 .
.  当
当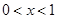 ,或
,或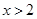 时,
时, 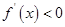 ; 6分
; 6分
当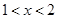 时,
时, 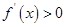 . 7分
. 7分 当
当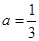 时,函数
时,函数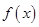 的单调增区间为
的单调增区间为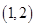 ;单调减区间为
;单调减区间为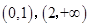 . 8分
. 8分
(如果把单调减区间写为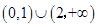 ,该步骤不得分)
,该步骤不得分)
(3)当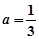 时,由(2)可知函数
时,由(2)可知函数 在
在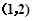 上为增函数,
上为增函数,
∴函数 在[1,2]上的最小值为
在[1,2]上的最小值为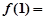
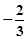 9分
9分
若对于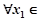 [1,2],
[1,2],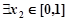 使
使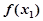 ≥
≥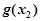 成立
成立
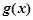 在
在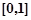 上的最小值不大于<
上的最小值不大于<

练习册系列答案
相关题目
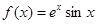 .
. 的单调区间;
的单调区间;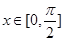 ,
,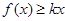 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;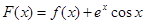 ,
,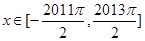 ,过点
,过点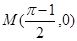 作函数
作函数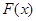 图象的所有切线,令各切点得横坐标构成数列
图象的所有切线,令各切点得横坐标构成数列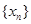 ,求数列
,求数列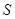 的值.
的值.
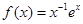 的定义域为
的定义域为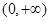 .
.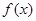 在
在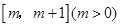 上的最小值;
上的最小值;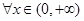 ,不等式
,不等式 恒成立,求
恒成立,求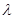 的取值范围.
的取值范围.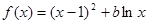 ,其中
,其中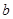 为常数。
为常数。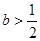 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;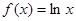
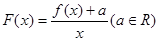 ,求
,求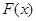 的极大值;
的极大值;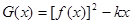 在定义域内单调递减,求满足此条件的实数k的取值范围.
在定义域内单调递减,求满足此条件的实数k的取值范围.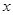 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量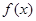 (万件)近似满足:
(万件)近似满足: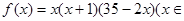 N*,且
N*,且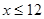 )
)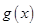 (万件)与月份
(万件)与月份 万件;
万件; 万件(不包含积压商品),要保证每月都满足供应,
万件(不包含积压商品),要保证每月都满足供应,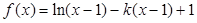 .
.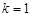 时,求函数
时,求函数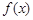 的最大值;
的最大值;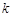 的取值范围;
的取值范围;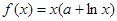 有极小值
有极小值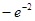 .
.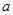 的值;
的值;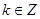 ,且
,且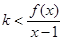 对任意
对任意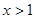 恒成立,求
恒成立,求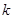 的最大值为.
的最大值为.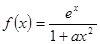 ,其中
,其中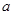 为正实数,
为正实数,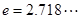 .
.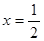 是
是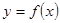 的一个极值点,求
的一个极值点,求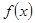 的单调区间.
的单调区间.