题目内容
已知函数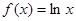
(Ⅰ)若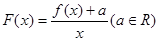 ,求
,求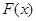 的极大值;
的极大值;
(Ⅱ)若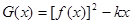 在定义域内单调递减,求满足此条件的实数k的取值范围.
在定义域内单调递减,求满足此条件的实数k的取值范围.
(Ⅰ)F(x)取得极大值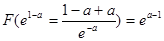 .(Ⅱ)
.(Ⅱ)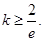
解析试题分析:(Ⅰ)利用“求导数,求驻点,讨论驻点左右区间的单调性,求极值”.
(Ⅱ)由G (x)在定义域内单调递减知: 在(0+∞)内恒成立.
在(0+∞)内恒成立.
通过构造函数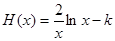 ,利用导数研究函数的单调性,确定H(x)取最大值
,利用导数研究函数的单调性,确定H(x)取最大值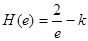
由 恒成立,确定得到实数k的取值范围.
恒成立,确定得到实数k的取值范围.
试题解析:(Ⅰ) 定义域为
定义域为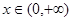
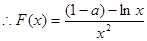 2分
2分
令 由
由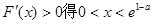
由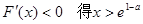 4分
4分
即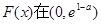 上单调递增,在
上单调递增,在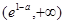 上单调递减
上单调递减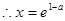 时,F(x)取得极大值
时,F(x)取得极大值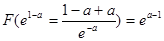 6分
6分
(Ⅱ)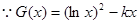 的定义域为(0+∞)
的定义域为(0+∞) 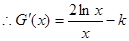
由G (x)在定义域内单调递减知: 在(0+∞)内恒成立 8分
在(0+∞)内恒成立 8分
令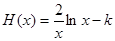 ,则
,则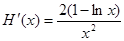 由
由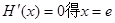
∵当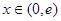 时
时 为增函数
为增函数
当 时
时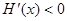
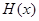 为减函数 10分
为减函数 10分
∴当x = e时,H(x)取最大值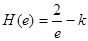
故只需 恒成立,
恒成立,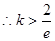
又当 时,只有一点x = e使得
时,只有一点x = e使得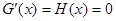 不影响其单调性
不影响其单调性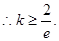 12分
12分
考点:利用导数研究函数的单调性、极值.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
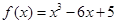 ,
,
 的单调区间;
的单调区间;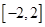 上的最值.
上的最值.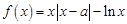 ,
,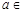
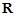 .
. ,求函数
,求函数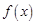 在区间
在区间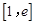 上的最值;
上的最值;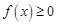 恒成立,求
恒成立,求 的取值范围. (注:
的取值范围. (注: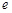 是自然对数的底数)
是自然对数的底数)
 时,求
时,求 的极值;
的极值;  上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围. 的图象如图,f(x)=6lnx+h(x).
的图象如图,f(x)=6lnx+h(x).
 )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;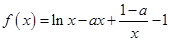 .
.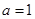 时,求曲线
时,求曲线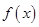 在
在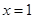 处的切线方程;
处的切线方程;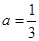 时,求函数
时,求函数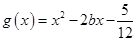 ,若对于
,若对于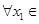 [1,2],
[1,2],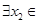 [0,1],使
[0,1],使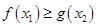 成立,求实数
成立,求实数 的取值范围.
的取值范围. 在
在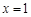 处取得极值.
处取得极值. 的值;
的值; 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
 ,使
,使 成立,求实数
成立,求实数 (
( ).
). 时,判断
时,判断 在定义域上的单调性;
在定义域上的单调性; 上的最小值为
上的最小值为 ,求
,求 的值;
的值; 在
在 上恒成立,试求
上恒成立,试求 ,它的一个极值点是
,它的一个极值点是 .
. 的值及
的值及 的值域;
的值域; ,试求函数
,试求函数 的零点的个数.
的零点的个数.