题目内容
已知二次函数f(x)=x2-2mx+1,若对于[0,1]上的任意三个实数a,b,c,函数值f(a),f(b),f(c)都能构成一个三角形的三边长,则满足条件的m的值可以是 .(写出一个即可)
【答案】分析:根据对于[0,1]上的任意三个实数a,b,c,函数值f(a),f(b),f(c)都能构成一个三角形的三边长可知只需当x∈[0,1]时,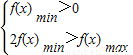 ,然后讨论m,求出满足条件的m的值即可.
,然后讨论m,求出满足条件的m的值即可.
解答:解:由题意当x∈[0,1]时,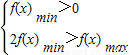 ;
;
当m≤0时,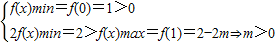 不存在;
不存在;
当m≥1时,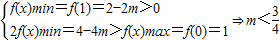 ,不存在;
,不存在;
当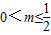 时,
时,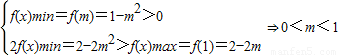 ,
,
所以这时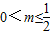 ;
;
当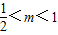 时,
时,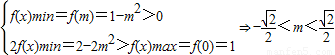 ,
,
所以这时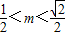 ;综上所述
;综上所述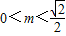 .
.
故答案为:0<m<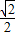 内的任一实数.
内的任一实数.
点评:本题主要考查了函数最值的应用,以及构成三角形的条件,同时考查了分类讨论的数学思想,属于中档题.
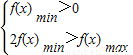 ,然后讨论m,求出满足条件的m的值即可.
,然后讨论m,求出满足条件的m的值即可.解答:解:由题意当x∈[0,1]时,
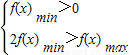 ;
;当m≤0时,
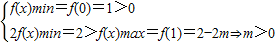 不存在;
不存在;当m≥1时,
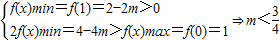 ,不存在;
,不存在;当
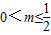 时,
时,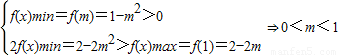 ,
,所以这时
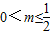 ;
;当
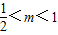 时,
时,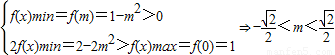 ,
,所以这时
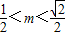 ;综上所述
;综上所述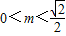 .
.故答案为:0<m<
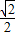 内的任一实数.
内的任一实数.点评:本题主要考查了函数最值的应用,以及构成三角形的条件,同时考查了分类讨论的数学思想,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目