题目内容
已知命题:①函数f(x)=
 在(0,+∞)是减函数;
在(0,+∞)是减函数;②函数f(x)的定义域为R,f′(x)=0是x=x为极值点的既不充分又不必要条件;
③在平面内,到定点(2,1)的距离与到定直线3x+4y-10=0的距离相等的点的轨迹是抛物线;
④函数f(x)=2sinxcos|x|的最小正周期是π;
⑤已知
 ,则
,则 在
在 方向上的投影为4.
方向上的投影为4.其中正确命题的序号是 .
【答案】分析:①从定义域入手;
②从极值点的定义入手,举出具体函数的例子说明;
③根据抛物线的定义就可得出;
④从y=cosx为偶函数入手,绝对值符号无影响;
⑤根据投影的计算公式计算.
解答:解:①错,因为x=1时,lgx=0,此时f(x)无意义;
②对,例如:f(x)=x3,f′(0)=0,但x=0不是极值点,又如:f(x)=|x|,x=0是极小值点,但x=0处不可导;
③错,因为定点(2,1)就在定直线3x+4y-10=0上,所以轨迹是两个点.
④对,∵f(x)=2sinxcos|x|=2sinxcosx=sin2x,故最小正周期为π
⑤错,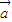 在
在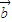 方向上的投影=
方向上的投影=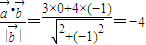
故答案为:②④
点评:本题主要考查了一些数学的定义,体现了数学的严格性.
②从极值点的定义入手,举出具体函数的例子说明;
③根据抛物线的定义就可得出;
④从y=cosx为偶函数入手,绝对值符号无影响;
⑤根据投影的计算公式计算.
解答:解:①错,因为x=1时,lgx=0,此时f(x)无意义;
②对,例如:f(x)=x3,f′(0)=0,但x=0不是极值点,又如:f(x)=|x|,x=0是极小值点,但x=0处不可导;
③错,因为定点(2,1)就在定直线3x+4y-10=0上,所以轨迹是两个点.
④对,∵f(x)=2sinxcos|x|=2sinxcosx=sin2x,故最小正周期为π
⑤错,
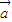 在
在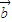 方向上的投影=
方向上的投影=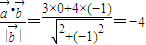
故答案为:②④
点评:本题主要考查了一些数学的定义,体现了数学的严格性.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目