题目内容
设集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},
(1)若A∩B=B,求实数m的取值范围;
(2)当x∈R时,没有元素x使得x∈A与x∈B同时成立,求实数m的取值范围.
解:(1)∵A∩B=B,∴B⊆A
当m+1>2m-1,即m<2时,B=∅,满足B⊆A.
当m+1≤2m-1,即m≥2时,要使B⊆A成立,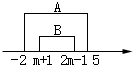
需 ,可得2≤m≤3,
,可得2≤m≤3,
综上,m≤3时有A∩B=B.
(2)因为x∈R,且A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},又没有元素x使x∈A与x∈B同时成立,
∴A与B交集为空集.
∴①若B=∅,即m+1>2m-1,得m<2时满足条件;
②若B≠∅,则要满足的条件是
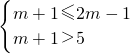 或
或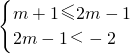 ,
,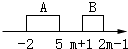
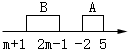
解得m>4.
综上,有m<2或m>4.
分析:(1)若A∩B=B,则B⊆A,即说明B是A的子集,分B=∅与B≠∅讨论,即可求得实数m的取值范围;
(2)当x∈R时,没有元素x使x∈A与x∈B同时成立,则说明A与B交集为空集,再分B=∅与B≠∅讨论,即可求得实数m的取值范围.
点评:利用集合的关系,建立不等关系,求解参数问题,注意集合B能否是空集,必要时要进行讨论是解决这类问题的关键.
当m+1>2m-1,即m<2时,B=∅,满足B⊆A.
当m+1≤2m-1,即m≥2时,要使B⊆A成立,

需
 ,可得2≤m≤3,
,可得2≤m≤3,综上,m≤3时有A∩B=B.
(2)因为x∈R,且A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},又没有元素x使x∈A与x∈B同时成立,
∴A与B交集为空集.
∴①若B=∅,即m+1>2m-1,得m<2时满足条件;
②若B≠∅,则要满足的条件是
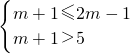 或
或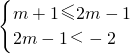 ,
,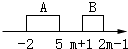

解得m>4.
综上,有m<2或m>4.
分析:(1)若A∩B=B,则B⊆A,即说明B是A的子集,分B=∅与B≠∅讨论,即可求得实数m的取值范围;
(2)当x∈R时,没有元素x使x∈A与x∈B同时成立,则说明A与B交集为空集,再分B=∅与B≠∅讨论,即可求得实数m的取值范围.
点评:利用集合的关系,建立不等关系,求解参数问题,注意集合B能否是空集,必要时要进行讨论是解决这类问题的关键.

练习册系列答案
相关题目